FORMIND - Introduction
FORMIND is an individual-based, spatially explicit and process-based model designed for simulating species-rich vegetation communities (Fischer et al. 2016).
In FORMIND, vegetation is simulated on an area of size $A_\text{area}$, which is a composite of regularly ordered, quadratic patches of size $A_\text{patch} \, \left[ \text{m}^2\right]$ described by their location within the area (figure below). Individual trees grow within the patches, but do not have spatially explicit positions within a patch (the gap model approach).
Figure: Illustration of the simulated area and its composition of regularly ordered patches. Individual trees do not have spatially explicit positions within the patches. Only for an illustrative purpose, we show positioned trees on an exemplary patch.
The trees change their sizes during the simulation according to a set of ecophysiological and morphological parameters used within the modelled processes. The modelled processes are simulated on different levels: (i) area-level, (ii) patch-level or (iii) single-tree level.
The individual model components are described in the following subpages:
- Geometry: trees are described via several geometric relationships. Tree types (in some projects we use the concept of plant functional types and in others real species) can differ in their parameter sets of these relationships.
Within each time step $\Delta t$ (e.g. one year), the following main processes considered:
-
Recruitment and establishment: Establishment of recruited seeds is modelled on the patch level, whereby the distribution of seeds is simulated on the area level.
-
Mortality: First, an event-driven mortality due to crowding can take place on the patch level. Afterwards, mortality rates affects each trees (e.g. base mortality). Finally, every dying tree may fall and damage other trees.
-
Environment: The patches of the simulation area are homogeneous regarding climatic input variables. Based on these input parameters, the environment of the trees is specified. For example, the radiation above canopy and day length are equal for all patches. The vertical attenuation of the incoming radiation (i.e. light climate) is calculated for each patch based on the vegetation state, so that light intensity at different heights can differ between patches dependent on the number of trees shading each other. Reduced light availability results in reduced gross photosynthesis of a tree. Limited soil water resources can also reduce the gross photosynthesis of an individual. In the same manner as the light climate, soil water contents can differ between patches during the simulation, although the initial soil water content and other soil properties (e.g. soil porosity) are equal for all patches. Differences in soil water content between patches are dependent on the number of trees per patch, which take up soil water resources. Further, type-specific effects of the air temperature can also limit gross photosynthesis and affect respiration of an individual.
-
Growth: growth of a single tree is determined by its gross productivity, respiration and type-specific morphological parameters. Respiration is calculated on the level of an individual. An increase in biomass per tree is modelled as the difference between gross photosynthesis and respiration. The allocation of the resulting biomass (including the increase of geometrical properties according to chapter Geometry) act on the level of a tree.
-
Disturbance: Fire and landslide events are simulated on the areaa level.
-
Logging: Selective logging of trees is simulated on the area level. The selection is based on tree-specific characteristics (e.g. stem diameter or tree type) and represent conventional or reduced impact logging.
The modelled processes, which are summarized within the above mentioned main processes, are scheduled in a serial way. For an overview on the modelled processes and their schedule, see the figure below:
Figure: Block diagram of the modelled processes.
Different colours indicate the spatial scale on which each process is
calculated (blue = area, green = patch, orange= individual). Italic
written boxes show processes which are simulated with time steps of
higher resolution than $\Delta t$ (e.g one year). Numbers
in brackets within each box show the serial order of their calculation
within one time step $\Delta t$. Grey frames that
underly these boxes group them according to the above mentioned main
processes and their corresponding chapters. Rhombuses indicate climatic input parameters with the following abbreviations: PET – potential evapotranspiration, PPFD – photoactive photon flux density.
Periodic or open boundary conditions can be used. For periodic boundary conditions, that means processes leaving one side of the simulation area are entering the area on the opposite side again. For open boundary conditions, that means processes leaving the simulation area are lost. No migration entering the open boundaries would be considered.
For the purpose of calculations within the processes of light climate and crowding mortality, the above-ground space is discretized into vertical height layers of constant width $\Delta h$. The table below shows general input parameters.
| Description | Parameter | Unit | values range |
|---|---|---|---|
| Time step | $\Delta t$ | $\text{yr}$ | $365^{-1} - 5$ |
| Simulation area | $A_{\text{area}}$ | $\text{ha}$ | $1-400$ |
| Patch area | $A_{\text{patch}}$ | $\text{m}^2$ | $400$ |
| Width of height layers | $\Delta h$ | $\text{m}$ | $0.5$ |
Geometry
- Height - Stem Diameter - Relationship
- Crown length - Height - Relationship
- Crown diameter - Stem diameter - Relationship
- Crown area - Crown diameter - Relationship
- Aboveground biomass - Stem diameter - Relationship
- Leaf area index - Stem diameter - Relationship
- Maximum Values
Although individual trees in real forests do not necessarily have identical shapes, we model each tree by a cylindrical stem and a cylindrical crown (see figure below). The geometry of an individual can be described completely by the following size characteristics: stem diameter ($D$), height ($H$), crown diameter ($C_\text{D}$), crown length ($C_\text{L}$) and crown projection area ($C_\text{A}$) as shown in the figure below.
Figure: Geometrical representation of a single tree . The following abbreviations describe size characteristics of the modelled tree geometry: $D$ -stem diameter, $H$ - height, $C_\text{D}$ - crown diameter, $C_\text{L}$ - crown length, $C_\text{A}$ crown projection area.
These size characteristics are functionally related to each other. In the following, we describe the functional relationships used. Parameters of the described relationships can vary between different tree types. Some graphical examples are given in figure at the end of the page.
Height - Stem Diameter - Relationship
The height $H\,[\text{m}]$ of an tree relates to its stem diameter $D\,[\text{m}]$ by several approaches. $h_\text{0}$, $h_\text{1}$ and $h_\text{2}$ are type-specific parameters.
Polynomial approach
\begin{equation} H=h_0+h_1 \cdot D+h_2 \cdot D^2 \end{equation}
Saturation approach
\begin{equation} H=\frac{D}{\frac{1}{h_0}+\frac{D}{h_1}} \end{equation}
Power-law approach
\begin{equation} H=h_0 \cdot D^{h_1} \end{equation}
Crown length - Height - Relationship
The crown length $ C_L \, [\text{m}]$ of a tree is modelled as a fraction of its height $ H\, [\text{m}]$. $c_\text{l0}$, $c_\text{l1}$ and $c_\text{l2}$ are type-specific parameters.
Linear approach (most frequently used)
\begin{equation} C_L=c_{l0} \cdot H \end{equation}
Saturation approach
\begin{equation} C_L=(-\frac{c_{l0} \cdot H \cdot c_{l1}}{c_{l0}\cdot H + c_{l1}} + c_{l2}) \cdot H \end{equation}
Polynomial approach
\begin{equation} C_L=(c_{l0} + c_{l1} \cdot H + c_{l2} \cdot H^2) \cdot H \end{equation}
Crown diameter - Stem diameter - Relationship
The second dimension of the cylindrical crown, i.e. the crown diameter $C_D\,[\text{m}]$ of a tree relates to its stem diameter $D\,[\text{m}]$ by several approaches. $c_\text{d0}$, $c_\text{d1}$ and $c_\text{d2}$ are type-specific parameters.
Exponential approach I
\begin{equation} C_D = D \cdot \left(c_{d0} + c_{d1} \cdot exp\left(-c_{d2} \cdot D\right) \right) \end{equation}
Exponential approach II
\begin{equation} C_D = c_{d0} \cdot D + c_{d1} \cdot exp\left(-c_{d2} \cdot D\right) \end{equation}
Polynomial approach
\begin{equation} C_D = c_{d0} + c_{d1} \cdot D + c_{d2} \cdot D^2 + c_{d3} \cdot D^3 \end{equation}
Linear approach
\begin{equation} C_D = c_{d0} \cdot D \end{equation}
Saturation approach
\begin{equation} C_D = \frac{D}{\frac{1}{c_{d0}}+\frac{D}{c_{d1}}} \end{equation}
Power-law approach (most frequently used)
\begin{equation} C_D = c_{d0} \cdot D^{c_{d1}} - c_{d2} \end{equation}
Crown area - Crown diameter - Relationship
The crown projection area $C_A \, [\text{m}^2]$ of a tree is simply the ground area of the modelled cylindrical crown: \begin{equation} C_A=\frac{\pi}{4} \cdot C_D^2 \end{equation}
Aboveground biomass - Stem diameter - Relationship
The aboveground volume of a tree captures biomass (i.e. organic dry matter). The following different ways of modelling the aboveground biomass are included in FORMIND.
Geometrical approach (most frequently used)
Aboveground biomass $B\,[t_\text{odm}]$ of a tree is calculated in relation to its stem diameter $D\,[\text{m}]$ and height $H\,[\text{m}]$ by: \begin{equation} B = \frac{\pi}{4} \cdot D^2 \cdot H \cdot f \cdot \frac{\rho}{\sigma} \end{equation}
whereby the calculation simply represents the volume of the stem (according to its geometry) multiplied by three factors, which describe the biomass content more concisely.
Firstly, $f\,[\text{-}]$ denotes a type-specific form factor, which accounts for deviations of the stem from a cylindrical shape. Secondly, the parameter $\rho\,[t_\text{odm}/\text{m}^3]$ represents the wood density, which describes how much organic dry matter per unit of volume the stem contains. Thirdly, the division by the parameter $\sigma\,[-]$, which represents the fraction of total aboveground biomass attributed to the stem, results then in the total aboveground biomass $B$.
In contrast to the constant parameters $\rho$ and $\sigma$, the form factor $f$ can change during the growth of a tree with respect to its stem diameter $D\,[\text{m}]$ via
\begin{equation} f=f_0 \cdot exp\left(f_1 \cdot D^{f_2}\right) \end{equation}
or
\begin{equation} f=f_0 \cdot D^{f_1} \end{equation}
$f_\text{0}$, $f_\text{1}$ and $f_\text{2}$ are type-specific parameters.
Power-law approach
Aboveground biomass $B\,[t_\text{odm}]$ of a tree can also be modelled in relation to its stem diameter $D\,[\text{m}]$ by:
\begin{equation} B =b_{0} \cdot D^{b_1} \end{equation}
whereby $b_0$ and $b_1$ are type-specific parameters.
Logarithmic approach
Aboveground biomass $B\,[\text{t}_{odm}]$ of a tree can also be modelled in relation to its stem diameter $D\,[m]$ by:
\begin{equation} B =exp \left(b_{0} \cdot (log(D)-b_{2}) \cdot \frac{2 \cdot b_{1}+(log(D)-b_{2})}{b_{1} +(log(D)-b_{2})}\right) \end{equation}
whereby $b_0$, $b_1$ and $b_2$ are type-specific parameters.
Leaf area index - Stem diameter - Relationship
In general, aboveground biomass is divided between woody biomass captured in the stem and green biomass captured in the crown leaves. Important for the photosynthetic production of a tree is the green biomass captured in crown leaves. As leaves absorb radiation for photosynthesis, the total amount of one-sided leaf area per unit of crown projection area (i.e. the individual's leaf area index) is of main interest. The leaf area index $LAI\,[\text{m}^2/{m}^2]$ of a tree relates functionally to its stem diameter $D\,[m]$ by:
Power-law approach (most frequently used)
\begin{equation} LAI =l_0 \cdot D^{l_1} \end{equation} whereby $l_0$ and $l_1$ are type-specific parameters.
Linear approach
\begin{equation} LAI =l_0 + l_1 \cdot D \end{equation} whereby $l_0$ and $l_1$ are type-specific parameters.
The figure below shows all modeled functional relationships with exemplary parameters.
Figure: Illustration of the modelled functional relationships, which are used to describe the geometry of a single tree. The approaches are in all cases the most frequently used ones. As parameters here we use the mean values of the parameter range, documented in table below.
| parameter | values range | unit |
|---|---|---|
| $H_{\max}$ | 15 - 55 | $\text{m}$ |
| $h_0$ | 2 - 7 | - |
| $h_1$ | 0.2 - 0.7 | - |
| $c_{l0}$ | 0.3 - 0.4 | - |
| $c_{d0}$ | 0.5 - 0.6 | - |
| $c_{d1}$ | 0.65 - 0.75 | - |
| $c_{d2}$ | 0.0 - 0.3 | - |
| $\rho$ | 0.4 - 0.8 | $\tfrac{t_{\text{odm}}}{m^{3}}$ |
| $\sigma$ | 0.7 | $\tfrac{t_{\text{odm}}}{t_{\text{odm}}}$ |
| $f_0$ | 0.75 - 0.80 | - |
| $f_1$ | -0.15 - -0.20 | - |
| $l_0$ | 1 - 3 | - |
| $l_1$ | 0.1 - 0.3 | - |
Table: Summary of the parameter range based on tropical parameterizations.
Maximum Values
The trees cannot grow indefinitely in FORMIND. We introduce the following maximum values for a plausible geometry of a mature individual:
- maximum stem diameter $D_{\text{max}} [\text{m}]$
- maximum height $H_{\text{max}} [\text{m}]$
Either the maximum stem diameter or the maximum height is given as a type-specific input parameter. The missing maximum value and the corresponding maximum biomass $B\,[t_\text{odm}]$ are then derived using the functional relationships mentioned in section h-d-relationship and section b-d-relationship. The maximum values are used in section growth.
Recruitment and Establishment
- Global in-growth rates
- Seed production and dispersal of mother trees
- Germination of seeds
- Establishment of seedlings
FORMIND 3.0 includes two different possibilities to model recruitment:
- by using global constant in-growth rates or
- by seed production and dispersal of mother trees.
Global in-growth rates
The number of recruited seeds is assumed to be brought into the local community from an intact forest community surrounding the simulated area. This number $N_{\text{seed}} [\frac{1}{\text{yr ha}}]$ is thereby a constant type-specific parameter independent of the density of individuals already existing on the simulated area.
The recruited seeds directly enter the seed pool, but they may only germinate and establish in the next time step. Each patch is assigned an own seed pool. The recruited seeds are distributed uniformly across the patches and added to the corresponding seed pool in an amount of
\[ N_{\text{pool}} = \left\lfloor \frac{N_{\text{seed}}}{\text{#patches}} \right\rfloor \]
If the number of ingrowing seeds $ N_{\text{seed}} $ is not a multiple of the number of patches #patches, a certain number of seeds will remain which are distributed randomly to the patches. For this, the patches are considered one by one incrementally starting with the first. Within each considered patch and for each remaining seed, which has not been distributed yet, its probability of assignment to the currently considered patch is compared with a random number (uniformly distributed in [0;1]). In the case of successful assignment (i.e. random number $ \leq $ 1/#patches), the seed number per patch $ N_{pool} $ is incremented and the number of remaining seeds decremented. At the end, the last patch receives all remaining seeds.
Before the start of the simulation, $ N_{\text{init}} $ seeds already existing in the seed pool per patch (i.e. $ N_{\text{pool}} $ = $ N_{\text{init}} $ ) can be defined for each type, which may germinate and establish as seedlings already in the first time step.
Seed production and dispersal of mother trees
Before the start of the simulation, it is obligatory to assign to the seed pool of each patch a type-specific number of seeds $ N_{\text{init}} $.
During the simulation, each individual of a cohort per patch is able to produce a predefined type-specific number of seeds $ N_{\text{seed}} $ on its own as a mother plant if it reaches apredefined stem diameter $ D_{\text{rep}} $. These produced seeds are dispersed among the neighboring patches surrounding that patch the mother plant is located in. The dispersal is dependent on a defined dispersal kernel, the crown diameter $ C_D $ of the mother plant and a predefined type-specific average dispersal distance $ dist $.
There is no distinction between different dispersal agents (e.g. wind, birds, mammals). The dispersal kernel is assumed to be Weibull distributed with a shape parameter of 2 and a scale parameter of $ (dist + C_D / 2)^2 $. Presuming rotation symmetry, the probability density $ f_{\text{disp}} $ that seeds are dispersed at a distance $r$ from the mother plant is defined as
\[ f_{\text{disp}}(r) = \frac{2 \cdot r}{\left(dist + \dfrac{C_D}{2} \right)^2 } \cdot \exp\left({-\frac{r^2}{ \left( dist + \frac{C_D}{2} \right)^2 }} \right) \]
For each seed per mother plant per patch, a distance $r$ is stochastically drawn from the dispersal kernel $ f_{\text{disp}} (r) $. Using the calculated distance $r$ and a random direction $DIR$ (drawn from a uniform distribution in the range of [0°;360°]), the target coordinates of the dispersed seed are determined in the following way
\[ x_{\text{seed}} = x_{\text{ind}} + r \sin \left( 2\pi \frac{DIR}{360} \right) \]
\[ y_{\text{seed}} = y_{\text{ind}} + r \cos \left( 2\pi \frac{DIR}{360} \right) \]
where $ (x_{\text{ind}}, y_{\text{ind}}) $ is a randomly generated position of the mother plant within its corresponding patch and $ (x_{\text{seed}}; y_{\text{seed}}) $ is the calculated virtual position of the dispersed seed on the simulation area. As in FORMIND 3.0 individuals do not have spatially explicit positions within the patches, the corresponding patch number of the dispersed seed is calculated from the coordinates $ (x_{\text{seed}}; y_{\text{seed}}) $.
The sum of those produced seeds, which are dispersed to a certain patch are added first to its corresponding seed pool $ N_{\text{pool}} $ before they are able to germinate and establish in the next time step.
Germination of seeds
Before seeds can germinate from the seed pool and establish successfully, light and space conditions are checked. Per type a minimum number of seeds can be withheld in the seed pool, which is by default set to 0.
For determining the light conditions, the incoming irradiance on the floor is divided by the incoming irradiance above canopy (see section Competition and environmental limitations for their calculation). This results in the percentage of incoming irradiance on the floor $ I_{\text{floor}} $, which is possibly reduced due to shading of already existing individuals. Dependent on a minimum percentage of light $ I_{\text{seed}} $ required for seed germination and seedling establishment for each type, it is checked whether $ I_{\text{floor}} $ is sufficient:
$$ N_{\text{germ}} = \begin{cases} N_{\text{pool}} & I_{\text{floor}} \geq I_{\text{seed}} \\ 0 & I_{\text{floor}} < I_{\text{seed}} \end{cases} , $$
where $ N_{\text{germ}} $ is the number of germinated seedlings. If light requirements are not sufficient for seeds of a specific type, they remain in the seed pool and may germinate in future time step as far as conditions become favorable. By this, seeds may accumulate in the seed pool if light conditions remain unfavorable over a period of time.
Seeds waiting in the seed pool for favorable germination conditions may be affected by seed pool mortality. For each type a mortality rate $ M_{\text{pool}} \left[ \frac{1}{\text{yr}} \right] $ is defined prior to the start of the simulation. A rate of $ M_{\text{pool}} = 0$ represents, for example, an unlimited accumulation of seeds in times of unfavorable conditions. In contrast, a rate of $ M_{\text{pool}} = 1$ would not allow any accumulation of seeds in the seed pool.
The density of germinated seedlings can be regulated as well. To this end, for each type and patch, the number $ N_{\text{germ}} = 0$ is truncated at a predefined value $ max_{\text{dens}} $.
Establishment of seedlings
If light requirements are fulfilled for successful seedling germination, it is secondly checked whether enough space is available for their establishment. Germinated seedlings start with a predetermined stem diameter $ D_{\text{min}} $, irrespective of type or species. Using the chosen functional relationships describing the geometry of an individual (see section Geometry, their corresponding height $ H_{\text{min}} $ can be calculated. If space at the respective height is already filled by more than 100% with existing individuals, none of the germinated seedlings would be able to establish:
$$ N_{\text{est}} = \begin{cases} N_{\text{germ}} & CCA_l < 1 \\ 0 & CCA_l \geq 1 \end{cases},$$
where $ N_{\text{est}} $ is the number of successfully established seedlings and $ CCA_{l} $ denotes the cumulative crown area at the height layer $ l $ (of height $ \Delta h : [\text{m}] $) that corresponds to $ H_{\text{min}} $:
$$ l=\left\lfloor \frac{H_{\text{min}}}{\Delta h} \right\rfloor. $$
See section Mortality for the calculation of the cumulative crown area $ CCA $ of all height layer of the aboveground discretized space.
Mortality
- Modelling tree mortality
- General mortality
- Crowding mortality
- Tree fall mortality
- Change of mortality due to fragmentation
- Overall change in number of trees per cohort
Modelling tree mortality
In FORMIND trees can die due to various reasons. The following different types of mortality occur in a serial way:
- background mortality $M_B$
- mortality dependent on an individual's stem diameter $M_D$
- mortality dependent on an individual's diameter increment $M_I$
- crowding mortality due to limited space
- mortality due to damage by a falling tree
- mortality due to fragmentation
Individual trees of the same type and size that are located in the same patch are summarized in this section by a so-called cohort. Each cohort is uniquely described by its type, the number of identical trees ($N$), their age and the size of one single tree (i.e. aboveground biomass). In this section, the number of identical trees in a cohort changes due to mortality processes. Below, we describe the different types of mortality in greater detail.
General mortality
In contrast to the event-driven forms of mortality we will describe later, there is a general mortality rate per tree which is active in each time step $t_y$. This mortality rate $M$ is calculated as the sum of the background mortality rate $M_B$ and two further mortality rates dependent on the stem diameter $M_D$ as well as its increment $M_I$:
\[ M = M_B + M_D + M_I .\]
The background mortality $M_B$ $[\frac{1}{\text{yr}}]$ is a type-specific constant input parameter.
The mortality rate $M_D$ depends on the stem diameter $D \, [\text{m}]$ and provides the possibility to give older trees (with a bigger stem diameter) a higher mortality rate than younger trees or vice versa. The rate is calculated via
\[M_D(D) = m_{d0} \cdot D^{m_{d1}},\]
where $m_{d0}$ and $m_{d1}$ are type-specific parameters.
The mortality rate $M_I$ depends on the increment of the stem diameter $D$ $[\text{mm}]$ per time step $t_y$ and provides the possibility to include a higher mortality for older trees or those under stress. It is modelled by the functional relationship
\[M_I(\Delta D) = m_{i0} + m_{i1} \Delta D + m_{i2} {\Delta D}^2 , \]
where $ m_{i0}$, $ m_{i1}$ and $ m_{i2}$ are type-specific parameters. The increment of the stem diameter from time $t$ to time $t + ty$ is denoted as $\Delta D$.
The trees per patch die according to their mortality rate $M$ - either stochastically or deterministically.
Deterministic dying is active if the number of individuals per cohort is greater than a predefined number $N_M$ and if the stem diameter of each individual is smaller than a predefined threshold $D_M$. In this case, the number of dying trees per cohort is determined by
\[N_Y = N \cdot M, \]
where $N$ is the number of trees in this cohort, $N_Y$ is the number of dying trees per cohort and $M$ is the calculated mortality rate per time step $t_y$. The number of dying trees $N_Y$ is rounded to $\lfloor N_Y + 0.5 \rfloor$.
In the contrary case (i.e. $N < N_M$ or $D > D_M$), deaths occur stochastically. That means, for each tree the mortality rate $M$ represents its probability of dying (i.e. by comparing a random number from a uniform distribution in the range of $[0;1]$ with the mortality rate $M$):
\[N_Y = \sum_{j=1}^N \delta_{rM},\]
where $N$ is the number of trees per cohort, $N_Y$ is the number of dying trees per cohort, $M$ is the calculated mortality rate per time step $t_y$ and $r$ is a random number from a uniform distribution in the range of $[0;1]$. The symbol $\delta_{rM}$ is defined as
\[\delta_{rM} = \begin{cases} 1 & \text{, } r \leq M \\ 0 & \text{, } r > M \end{cases}.\]
Crowding mortality
Crowding occurs if at any height layer the cumulative crown area of all trees on a patch exceeds $A_\text{patch}$. At first, the cumulative crown area $CCA$ $[\frac{m^2}{m^2}]$ of all trees on a patch is calculated for each height layer $i$ relative to the patch area $A_\text{patch}$:
\[CCA_i = \frac{1}{A_\text{patch}} \cdot \sum_{\text{all individuals} \ \text{with } l_{min} \leq i \leq l_{max}} C_A,\]
where $C_A$ is the crown projection area of a tree (see section B). Each tree occupies only a limited amount of height layers (i.e. between layer $l_\text{min}$ and $l_\text{max}$) defined by the individual's crown length $C_L [\text{m}]$ and its height $H [\text{m}]$:
\[l_\text{max}= \left\lfloor \frac{H}{\Delta h} \right\rfloor \ l_\text{min}= \left\lfloor \frac{H-C_L}{\Delta h} \right\rfloor \]
Mortality due to crowding is calculated per tree and represented by a reduction factor $Rc$ $[-]$. This individual reduction factor is calculated based on those height layers that the individual's crown is occupying (see Figure below).
Figure: Illustration of crowding on the example of two single trees. The limits of each crown are shown by $l_\text{min}(\text{Tree 1})$, $l_\text{max}(\text{Tree 1})$, $l_\text{min}(\text{Tree 2})$ and $l_\text{max}(\text{Tree 2})$. The vertically discretized aboveground space into height layers of width $\Delta h$ $[\text{m}]$ is coloured differently according to the sum of the crown projection areas of both individuals occupying the layers. The darker the colour is, the more crowns occupy the respective height layer. This is calculated by the cumulative crown area $CCA$ $[-]$ relative to the patch area, which is illustrated on the right side. The maximum of $CCA$ is used to calculate the reduction factor $R_c$ for each individual. In this example, the reduction factor for each of both trees is calculated based on the 5th height layer from the bottom (equal to layer $l_\text{min}(\text{Tree 1})$ and $l_\text{max}(\text{Tree 2})$).
The reduction factor $R_c$ is determined by the reciprocal of the maximum cumulative crown area $CCA$ corresponding to the height layers between the individual limits $l_\text{min}$ and $l_\text{max}$:
\begin{align} R_c = \frac{1}{\max\limits_{i \in [l_\text{min}, ..., l_\text{max}]} (CCA_i)}. \end{align}
If the maximum cumulative crown area of any height layer that the individual's crown is occupying exceeds $A_\text{patch}$ (i.e. $CCA_i > 1$), the individual reduction factor $R_c$ falls below the threshold of $0.99$. In this case, the number of dying identical trees per cohort $N_C$ is calculated by
\[N_C = N~(1-R_c).\]
Mortality due to crowding (or self-thinning) can be interpreted as competition for space. Besides crowding, the vertical discretization of the aboveground space is also important for the light climate calculations. To save computation time, the calculation of $R_c$ is coupled to that of the light climate, which is explained in Chapter E.
Tree fall mortality
If a tree falls, neighboring trees can be destroyed. A dying tree falls down with probability $f_{fall}$. The falling target patch depends on the falling direction and on the tree height $H$. The falling direction $DIR$ (drawn from a uniform distribution in the range of $[0, 360]$) is chosen randomly. The target coordinates of the falling tree $(x_{fall}; y_{fall})$ are determined in the following way:
\begin{align}
x_\text{fall} &= x_\text{tree}+H\sin\left(2~\pi~\frac{DIR}{360}\right) \\
y_\text{fall} &= y_\text{tree}+H\cos\left(2~\pi~\frac{DIR}{360}\right)
\end{align}
where $(x_\text{tree}; y_\text{tree})$ is the standing position of the falling tree. These target coordinates are used to determine the affected patch. All smaller trees ($\text{tree height} < H$) in this target patch are dying with a damage probability $M_\text{dam}$:
\begin{align} M_\text{dam} = \frac{C_A}{A_\text{patch}} , \end{align}
where $C_A$ is the crown area of the falling tree and $A_\text{patch}$ the area of the target patch.
The trees in the target patch die according to the damage rate $M_\text{dam}$ - either stochastically or deterministically. Deterministic dying is active if the number of trees per cohort is greater than $100$. In this case, the number of dying trees per cohort $N_F$ is determined by multiplying the number of trees $N$ per cohort with the damage rate $M_\text{dam}$.
\begin{align} N_F = N \cdot M_\text{dam}, \label{NF} \end{align}
The number of dying trees $N_F$ is rounded to $\left\lfloor N_F + 0.5 \right\rfloor$.
In the contrary case (less than $100$ trees per cohort), stochastic dying is performed. That means, for each tree the damage rate $M_\text{dam}$ represents its probability of dying (i.e. by comparing a random number from a uniform distribution in the range of $[0;1]$ with the damage rate).
\begin{align} N_F = \sum_{j=1}^N \delta_{rM_\text{dam}} \text{,} \label{NF2} \end{align}
where $N$ is the number of trees per cohort, $N_F$ is the number of dying trees per cohort, $M_\text{dam}$ is the damage rate per time step $t_y$ and $r$ is a random number from a uniform distribution in the range of $[0;1]$. The symbol $\delta_{rM_\text{dam}}$ is defined as:
\begin{align} \delta_{rM_\text{dam}} = \begin{cases} 1 & \text{, } r \leq M_\text{dam} \\ 0 & \text{, } r > M_\text{dam} \end{cases} \label{deltarMdam} \end{align}
Change of mortality due to fragmentation
It has been observed that mortality is increased and tree species richness is reduced at forest edges, and that large trees are often missing in small fragments. The extent of forest edges varies between forest regions. For example, increased edge mortality could be measured up to $100 \text{m}$ into the forest interior in the Amazon.
In FORMIND we model increased mortality at the edge of forest fragments by multiplying the general mortality $M$ with a fragmentation variable $m_\text{frag}$. Thus, the additional mortality due to fragmentation can be calculated as
\begin{align} M_\text{frag}=M \cdot (m_\text{frag} - 1). \end{align}
We assume that the fragmentation-induced mortality $M_\text{frag}$ is higher at forest edges ($< 100 \,m$) than in the interior. Thus, the value of $m_\text{frag}$ is modelled dependent on the distance to the fragment edges (see Table below). In addition, large trees ($D > 60 \,\text{cm}$) can suffer an increased mortality.
| Distance to edge | Value of $m_\text{frag}$ ($D \leq 60$) | Value of $m_\text{frag}$ ($D > 60$) |
|---|---|---|
| 0 - 20 $\text{m}$ | 2.5 | 4 |
| 20 - 40 $\text{m}$ | 1.75 | 2.5 |
| 40 - 60 $\text{m}$ | 1.375 | 1.75 |
| 60 - 80 $\text{m}$ | 1.1875 | 1.375 |
| 80 - 100 $\text{m}$ | 1.09375 | 1.1875 |
Table: Mortality increase due to fragmentation, dependent on the distance to a fragment edge and on the stem diameter $D \, [\text{cm}]$ of a tree.
If this type of mortality is activated, we recommend to choose a patch size of $20 \,\text{m}$ x $20 \,\text{m}$ (i.e. $A_\text{patch} = 400 \,\text{m}^2$) according to the distance classes in the Table above.
The number of additional trees that die due to fragmentation effects can be calculated as:
\begin{align} N_\text{frag}=N \cdot M_\text{frag}. \end{align}
Overall change in number of trees per cohort
Overall, per time step $\Delta t$ and for each cohort the change in the number of trees per cohort $N$ is determined by:
\begin{align} \Delta N = -(N_Y + N_C +N_F + N_\text{frag}), \end{align}
where $N_Y$ is the number of trees dying due to regular mortality, $N_C$ is the number of trees dying due to crowding, $N_F$ is the number of trees dying due to damages caused by a falling tree and $N_\text{frag}$ is the number of trees dying due to increased mortality near fragment edges.
The amount of aboveground carbon $S_\text{mort}$ $[\frac{t_{C}}{\text{ha}}]$ resulting from the death of trees within the current time step is calculated by
\begin{align} S_\text{mort} = 0.44 \cdot \sum_\text{all cohorts} (N_Y + N_C + N_F + N_\text{frag})\cdot B, \end{align}
where $B$ is the aboveground biomass of the tree (see chapter Geometry). We assume that $1 \text{g}$ organic dry matter contains $44 \%$ carbon Larcher 2001.
Competition and environmental limitations
Light climate
A single tree on a patch receives full incoming radiation. An increasing number of individual trees of differing heights on a patch results in shading within the canopy. Higher trees intercept radiation, which is not available for smaller individuals. Thus, with decreasing height from the canopy down to the ground, radiation is decreasing. We call this vertical distribution of light availability within a patch ’light climate’.
To calculate the light availability in different heights within the canopy, the vertical discretization of the above-ground space is used (i.e. height layers of constant width $\Delta h$). For each patch and height layer, the leaf area accumulated by all trees on the patch is calculated. Each tree contributes parts of its crown leaf area to those height layers, which are occupied by its crown (i.e. height layers from $l_{min}$ to $l_{max}$). These limits are determined by the individual’s crown length $C_{L}$ and its height $H$: \[ l_{max}= \left\lfloor \frac{H}{\Delta h} \right\rfloor\\ l_{min}= \left\lfloor \frac{H-C_L}{\Delta h} \right\rfloor.\]
The number of height layers a tree is occupying by its crown $n_{layer}$ can then be calculated by: \[n_{layer} = l_{max}-l_{min}\]
For those height layers between $l_{min}$ and $l_{max}$, an individual’s leaf area contributes equally to each layer $i$: \[ \bar{L_{i}}=\frac{LAI \cdot C_A}{n_{layer}}, \]
whereby $ \overline{L_{i}} $ $[m²]$ represents the contribution of an tree’s leaf area to the layer $i$, $LAI~[-]$ is the leaf area index of the tree (see section B.6) and $C_{A}~[m²]$ is crown projection area of the tree’s crown. The multiplication of $LAI$ by $C_{A}$ results in the leaf area in $[m²]$ of a single tree .
Summing up all contributions of the trees’ leaf area per patch to their respective occupied height layers and relative to the patch area, results in the patch-based leaf area index $\hat{L_{i}}~[-]$ per layer $i$:
\[\hat{L_{i}} =\frac{1}{A_{patch}} \sum_{\ all\ individuals \\ with\ l_{min} \leq i \leq l_{max}} \hat{L_{i}},\] where $\hat{L_{i}}$ [m²] represents the leaf area contribution of an tree to the height layer $i$ and $A_{patch}~[m²]$ denotes the area of a patch.
Using this information, the radiation each tree is able to intercept can be determined. Light attenuation through the canopy is calculated using the approach of . The incoming radiation $I_{ind}$ on top of a tree (i.e. on top of the height layer $l_{max}$ the tree is reaching) is calculated by: \[ I_{ind}=I_{0}\cdot exp \left(-k \cdot \sum_{i>l_{max}}\hat{L_{i}}\right), \]
where the sum in the exponent accumulates the patch-based leaf area indices of all height layers above the individual’s height. The parameter $k$ denotes the light extinction coefficient $[-]$ of a tree, $I_{0}$ $[\mu mol (photons)/m² s]$ is the daily radiation above canopy averaged from sunrise to sunset during the vegetation period and $\hat{L_{i}}$ [-] represents the patch-based leaf area index of height layer $i$.
Figure 6: Illustration of the light climate on the example of two single trees . The limits of each crown are shown by $l_{min} (Tree1)$, $l_{max} (Tree1)$, $l_{min} (Tree2)$, $l_{max} (Tree2)$. The vertically discretized aboveground space into height layers of width $\Delta h$ $[m]$ is coloured differently according to the available radiation. The lighter the colour is, the more attenuated the radiation is, which results from the absorption by higher individuals' leaves. On the right hand side the decrease of available light from the canopy to the floor is illustrated by the grey polygon. Thereby, attenuation is greatest in the height layer both trees occupy by their crowns (i.e. layer $l_{min} (Tree1)$ and $l_{max} (Tree2)$.
By determining the available radiation for each single tree (at the top of the crown), competition for light between trees is considered.
Water cycle and soil water limitation
Individual trees take up soil water resources to fulfill the requirements for their gross productivity. We determine an individual's uptake of soil water based on its demand and on the total available soil water.
Firstly, the soil water content $\Theta_{soil}$ is computed preliminary on an hourly basis using a differential equation, which quantifies preliminary hourly changes in the soil water content per patch depending on precipitation $PR$, interception $IN$ and run-off $RO$ (see figure below, cf. Kumagai et al. 2004 ): \begin{equation} \tag{55} \frac{d \Theta_{soil}}{dt} = PR(t) - IN(t) - RO(t) .\ \label{SWC} \end{equation} The resulting soil water content represents the total available soil water before soil water uptake by individuals. Uptake of soil water resources by trees is modelled equal to their transpiration and subtracted from $\Theta_{soil}$ later within the timestep (see eqn. \ref{soilwater}).
The interception $IN~[mm/h]$ is calculated dependent on the total leaf area index per patch (i.e. $ \sum_{i} \hat{L_{i}}$ in $[-]$, cf. Liang et al. 1994): \begin{equation} \tag{56} IN(t) = \text{min}\left(K_{L} \cdot \left(\sum_{i} ~ \hat{L_{i}}\right), PR(t)\right), \label{in} \end{equation} where $K_{L}~[mm/h]$ is the interception constant and $PR~[mm/h]$ denotes the precipitation.
On the ground surface of a patch, we consider two different run-offs: surface run-off and subsurface run-off:
\begin{equation}
RO(t) = RO_{\rightarrow}(t) + RO_{\downarrow}(t),\
\end{equation}
where surface run-off $RO_{\rightarrow}~[mm/h]$ is defined in the following way:
\begin{equation}
RO_{\rightarrow} = \text{max} \left(0, \Theta _{soil}(t) + PR(t) - IN(t) - POR \right)
\label{rosur}
\end{equation}
with $POR~[mm/h]$ denoting the soil porosity (i.e. defined as the maximum water intake of the soil per patch).All additional incoming water is assumed to be surface run-off.
Figure 7: Illustration of the water cycle on the example of a single tree.
For the calculation of the subsurface run-off $RO_{\downarrow}$ due to gravitation, we use the Brooks-Corey relation (cf. Liang et al. 1994): \begin{equation} RO_{\downarrow} = K_{s} \cdot \left( \frac{\Theta_{\text{soil}} (t)-\Theta_{\text{res}}}{POR-\Theta_{\text{res}}} \right)^{\frac{2}{\lambda}+3}, \label{rosub} \end{equation} where $K_{s}[mm/h]$ is the fully saturated conductivity, $\Theta_{res}[mm/h]$ the residual water content, and $\lambda~[-]$ the pore size distribution index.
The preliminary soil water content $\Theta_{soil}$ represents the soil water content, which is available for the individuals' uptake or transpiration. To calculate the transpiration $TR~[mm/h]$ of all trees per patch, we use the water-use-efficiency concept (cf. Lambers et al. 2008): \begin{equation} TR=\frac{1}{A_{patch}} ~\sum_{\text{all trees}} \frac{GPP}{WUE}, \end{equation} whereby $GPP$ in $[g_{\text{ODM}}/h]$ denotes the hourly gross primary production of an individual on the patch (see section F). Please note, that we simulate $GPP$ per time step $t_y$. To calculate $GPP$ on an hourly basis, we divide $GPP$ $[g_{\text{ODM}}/\Delta t]$ by the number of hours within the time step $\Delta t$. The constant type-specific value $WUE$ in $[g_{\text{ODM}}/kg_{H_2O}]$ represents the water-use-efficiency parameter and $A_{\text{patch}} \text{m}^2$ the area of a patch.
The resulting transpiration $TR$ may be limited in three ways calculated in a serial way:
PET limitation
Transpiration can be limited by the potential evapotranspiration $PET \tfrac{\text{mm}}{\text{h}}$ and the interception $IN \tfrac{\text{mm}}{\text{h}}$ (calculated by eqn. \ref{in}):
\begin{equation}
TR_{new} =
\begin{cases}
TR(t) & \text{,} TR(t) \leq PET(t) - IN(t)\\
PET(t) - IN(t) & \text{,} TR(t) > PET(t) - IN(t)
\end{cases}
\end{equation}
Soil water limitation Transpiration can be limited by the preliminary soil water content $\Theta_{soil}~[mm/h]$ (calculated by eqn. \ref{SWC}) and the permanent wilting point $\Theta_{pwp}~[mm/h]$: \begin{equation} TR_{new}(\Theta_{soil})= \begin{cases} TR(t) & \text{,} \Theta_{soil}(t) - TR(t) \geq \Theta_{pwp} \\ \Theta_{soil}(t) - \Theta_{pwp} & \text{,} \Theta_{soil}(t) - TR(t) < \Theta_{pwp} \\ 0 & \text{,} \Theta_{soil}(t) \leq \Theta_{pwp} \end{cases}. \end{equation}
Competition for water Competition between trees can limit the transpiration in the following way: \begin{equation} TR = \varphi_{W}(\Theta_{soil}) \cdot TR(t), \label{actTR} \end{equation} where $\varphi_{W}$ [-] represents a reduction factor ranging between 0 and 1, depending on the actual soil water content.
The reduction factor $\varphi_{W}$ is calculated using the approach of Granier et al. 1999, which is based on the preliminary soil water content (calculated by eqn. \ref{SWC}): \begin{equation} \varphi_{W}(\Theta_{soil})= \begin{cases} 0 & \text{,} \Theta_{soil}(t) \leq \Theta_{pwp} \\ \frac{\Theta_{soil}(t)- \Theta_{pwp}}{ \Theta_{msw}-\Theta_{pwp}} & \text{,} \Theta_{pwp} < \Theta_{soil}(t) \leq \Theta_{msw} \\ 1 & \text{,} \Theta_{msw} < \Theta_{soil}(t) \end{cases}, \tag{64} \label{phiW} \end{equation} where $\Theta_{pwp}$ is the permanent wilting point in $[V\%]$ and $\Theta_{msw}$ is the minimum soil water content in $[V\%]$. For the purpose of the calculation of eqn. \ref{phiW} only, $\Theta_{soil}$ needs to be converted from $[mm/h]$ to $[V\%]$. Thereby, the soil is modelled down to a constant depth $[m]$ defined prior to the start of the simulation.
The minimum soil water content ($\Theta_{msw}$) is determined according to Granier et al. 1999 by:
\begin{equation}
\Theta_{msw} = \Theta_{pwp} + 0.4 (\Theta_{fc}-\Theta_{pwp})
\label{msw}
\end{equation}
whereby $\Theta_{fc}$ denotes the field capacity in $[V\%]$.
The soil water content in the next day step is then calculated by the difference between the preliminary soil water content (calculated by eqn. \ref{SWC}) and the (eventually limited) transpiration $TR$: \begin{equation} \tag{66} \frac{d\Theta_{soil}}{dt} = \Theta_{soil}(t) – TR(t). \label{soilwater} \end{equation}
Figure 8: Water limitation function. a) limitation of TR due to PET. b) limitation of TR due to Soil water. c) $\varphi_{water}$ as function of Soil water.
Temperature
The gross primary production $GPP~[t_{ODM}/t_y]$ of a tree (see section F) may be influenced by phenology (esp. in the temperate zone) and air temperature. Respiration for maintenance purposes of an individual (see section F) may also be affected by air temperature. The influence on both - gross productivity and respiration, is modelled using limitation factor, by which they are simply multiplied (see section F). In the following, we describe the calculations of these limitation factors:
Phenology
Individual trees make photosynthesis only during their photosynthetic active period. In the temperate zone, we distinguish between broad-leaf and needle-leaf trees. Only deciduous broad-leaf trees have two phenology phases: (i) a dormant phase during winter and (ii) a photosynthetic active period of $\varphi_{act}~[days]$ after bud-burst until fall (i.e. the vegetation period).
The date of bud-burst is reached, if the temperature sum (daily mean air temperatures $> 5°C$) since 1 January is higher than a critical temperature $T_{crit}$ (Sato et al. 2007): \begin{equation} T_{crit}= -68+638 ~e^{-0.01\cdot n}, \label{budburst} \end{equation} where $n$ is the number of days per time step $\Delta t$ with an air temperature below $5 °$ since 1 November of the previous year. This algorithm is based on the global distribution of leaf onset dates estimated from remote sensing data (Botta et al. 2000). The photosynthetic active period stops if the 10-day moving average of daily mean air temperatures falls below $9 °C$ (Sato et al. 2007).
In contrast to the broad-leaf trees, the photosynthetic active period $\varphi_{act}$ of needle-leaf trees amounts a complete year of 365 days (without any dormant phase).
In the tropical zone, we assume for all individuals irrespective of their type a complete photosynthetic active period with $\varphi_{act}=365$ days.
Temperature limitation of gross productivity
The gross primary production of a tree can be reduced due to air temperatures. A corresponding limitation factor $\varphi_{T}$ is calculated by averaging the reduction factors over the whole time step $\Delta t$: \begin{equation} \varphi_{T}= \frac{1}{n} ~ \sum_{1}^{n} \varphi_{T,l} \cdot \varphi_{T,h}, \label{lim_temp} \end{equation} where $n$ is the number of days per time step $\Delta t$ and the values $\varphi_{T,l}$ and $\varphi_{T,h}$ are the daily inhibition factors for low and high air temperatures (Gutiérrez & Huth 2012, Haxeltine & Prentice 1996).\
The reduction factor for low air temperatures $\varphi_{T,l}~[°C]$ is calculated by: \begin{equation} \varphi_{T,l}= \left(1+ e^{k_{0} \cdot k_{1} - T }\right)^{-1}, \label{temp_low} \end{equation} where $T~[°C]$is the daily mean air temperature and $k_{0}$ and $k_{1}$ are type-specific parameters.
These parameters $k_{0}$ and $k_{1}$ are calculated by: \begin{equation} k_{0} = \frac{2 ~ln(0.01/0.99)}{T_{CO_{2},l}-T_{cold}} \label{k0} \end{equation}
\begin{equation} k_{1} = 0.5 ~(T_{CO_{2},l}+ T_{cold}) \label{k1} \end{equation} where $T_{CO_{2},l}$ [$°C$] and $T_{cold}$ [$°C$] are type-specific parameters representing the lowest temperature limit for CO$_{2}$ assimilation and the monthly mean air temperature of the coldest month an individual can cope with, respectively.\
Similarly, the \textbf{inhibition factor for high air temperatures} $\varphi_{T,h}$ in $°C$ is calculated by: \begin{equation} \varphi_{T,h} = 1 - 0.01 \cdot e^{k_{2} ~ (T-T_{hot}) } \label{temp_high} \end{equation} where $k_{2}$ is a type-specific parameter, $T$ [$°C$] is the daily mean temperature and $T_{hot}$ [$°C$] is the type-specific mean temperature of the hottest month an individual can occur.\
The parameter $k_{2}$ is calculated as: \begin{equation} k_{2} = \frac{ln(0.99/0.01)}{T_{CO_{2},h}-T_{hot}}, \label{k2} \end{equation} whereby $T_{CO_{2},h}$ [$°C$] and $T_{hot}$ [$°C$] are type-specific parameters representing the higher temperature limit for CO$_{2}$ assimilation and the monthly mean air temperature of the warmest month an individual can cope with, respectively.
Temperature limitation of maintenance respiration
Maintenance respiration is assumed to change exponentially with air temperature represented by the limitation factor $\kappa_{T}$ (Prentice et al. 1993):
\begin{equation} \kappa_{T} = \frac{1}{n} ~ \sum_{1}^{n} Q_{10}^{\left(\frac{T-T_{ref}}{10}\right)}, \label{r_main} \end{equation} where $n$ is the number of days per time step $t_y$, $T$ $[°C]$ is the daily mean air temperature, $Q_{10}$ $[-]$ and $T_{ref}$ $[°C]$ are constant parameters, irrespective of type. $T_{ref}$ represents the reference temperature, at which maintenance respiration is not influenced. Air temperatures below $T_{ref}$ result in a decrease of maintenance respiration ($\kappa_{T} < 1$) and those above $T_{ref}$ in an increase of maintenance respiration ($\kappa_{T} > 1$).
Figure 9: Temperature limitation function. a) limitation factor of Photosynthesis. b) limitation factor of maintenance respiration.
Growth of a tree
- Interim photosynthesis
- Gross primary production
- Biomass increment of a tree
- Maintenance respiration
- Maximum diameter growth curve
Interim photosynthesis
Based on the incoming irradiance on top of a tree $I_{ind}$ (see section Competition and environmental limitations), organic dry matter is produced via gross photosynthesis. In this section, the interim photosynthesis is calculated without reduction due to limited soil water availability and temperature effects.
The interim gross photosynthesis $P_{ind}$ of an individual is modelled using the approach of Thornley & Johnson 1990. It is based on the single-leaf photosynthesis modelled by a Michaelis-Menten function – a typical saturation function describing the relation between the radiation $I_{leaf}$ available on top of a leaf and its gross photosynthetic rate $P_{leaf}$: \begin{equation} P_{leaf}(I_{leaf}) = \frac{\alpha \cdot I_{leaf} \cdot p_{max}}{\alpha \cdot I_{leaf} + p_{max}}, \label{P_leaf} \tag{75} \end{equation} where $\alpha$ is the quantum efficiency, also known as the initial slope of the type-specific light response curve, $I_{leaf}$ is the incoming irradiance on top of the surface of a single leaf within the individual's crown and $p_{max}$ is the maximum leaf gross photosynthetic rate.
To obtain the incoming irradiance on top of the surface of a single leaf $I_{leaf}$, the available irradiance $I_{ind}$ on top of the entire individual has to be modified: \begin{equation} I_{leaf}(L) =\frac{k}{1-m} ~ I_{ind} \cdot e^{-k\cdot L}, \label{I_leaf} \end{equation} where $k$ [-] is the type-specific light extinction coefficient, $m$ [-] represents the transmission coefficient and $I_{ind}$ denotes the available incoming irradiance on top of a tree.
The first part $\frac{k}{1-m} ~ I_{ind}$ in the eqn. above is correcting the incoming irradiance in order to obtain those parts that can be absorbed by a leaf. The second part $e^{-k\cdot L}$ in the eqn. above accounts for self-shading within the individual's crown. As the leaves of an individual are assumed to be homogeneously distributed within its crown, some leaves will be shaded by higher ones within the crown. In this process, $L=0$ represents the top of the individual and $L=LAI$ represents the bottom of the individual's crown with $LAI$ being its leaf area index (see section Geometry).
To obtain the interim gross photosynthetic rate of a tree per year $P_{ind}$, the single-leaf photosynthesis of eqn. (\ref{P_leaf}) is integrated over the individual’s leaf area index $LAI$ (see section Geometry): \begin{equation} P_{ind} = \int_{0}^{LAI}P_{leaf}(I_{leaf}(L))dL.\ \label{P_tree} \end{equation}
The integration results in the interim photosynthesis of a tree per year (Thornley & Johnson 1990): \begin{equation} P_{ind} = \frac{p_{max}}{k} \cdot ln \frac{\alpha ~k~I_{ind} + p_{max}(1-m)}{\alpha ~k ~ I_{ind} ~ e^{-k \cdot LAI} + p_{max} (1-m)}. \label{P_tree_integral} \end{equation}
To convert the interim photosynthesis $P_{ind}$ from $[µmol_{CO_2}/m² s]$ to $[t_{ODM}/y]$, $P_{ind}$ has to be multiplied by the individual’s crown area $C_A$ (see section Geometry), the type-specific photosynthetically active period $\varphi_{act}$ and finally a conversion factor $c_{odm}$: \begin{equation} P_{ind} \cdot C_A \cdot 60 \cdot 60 \cdot l_{day} \cdot \varphi_{act} \cdot \varphi_{odm}, \label{GPP_tree} \tag{79} \end{equation} where the multiplication by $60 \cdot 60$ accounts for the conversion from seconds to hours. The factor $l_{day}$ [h] represents the mean day length during the vegetation period $\varphi_{act}$ [d] (see section Competition and environmental limitations). The conversion factor $\varphi_{odm} = 0.63 \cdot 44 \cdot 10^{-12}$ includes the molar mass of $CO_2$, the conversion from $g$ to $t$ and the conversion from $CO_2$ to organic dry mass $ODM$ (Larcher 2001).
Gross primary production
The gross primary production $GPP$ of a tree is calculated from the interim photosynthesis $P_{ind}$ [$t_{ODM}/y$] (see section Interim photosynthesis): \begin{equation} GPP = P_{ind} ~ \varphi_{T} ~\varphi_{W}, \label{GPP_tree2} \end{equation} where $\varphi_{W}$ denotes the reduction factor accounting for limited soil water and $\varphi_{T}$ represents the limitation factor of air temperature effect. Both factors range between 0 and 1 and thus, only reducing $GPP$ in times of unfavorable conditions (see section Competition and environmental limitations).
Biomass increment of a tree
Gross primary production $GPP$ of the eqn. above is first used for the maintenance of the already existing aboveground biomass of a tree. Costs for maintenance are modelled as biomass losses in terms of maintenance respiration $R_m$ [$t_{ODM}/y$]. The remaining productivity ($GPP-R_m$) is then available for growth of new aboveground biomass. Costs for the production of new structural tissue are modelled also as biomass losses in terms of growth respiration. This results in the net productivity $\Delta B$ (Dislich et al. 2009): \begin{equation} \Delta B = (1-r_g) ~(GPP - R_m) , \label{Binc} \end{equation} where $r_g$ [-] represents a constant parameter describing the fraction of ($GPP-R_m$) attributed to growth respiration. In contrast, maintenance respiration $R_m$ is modelled proportionally to the already existing aboveground biomass of a tree (see section Maintenance respiration).
Maintenance respiration
The maintenance respiration $R_{m}$ of a tree is calculated inversely by rearranging the eqn. above: \begin{equation} R_m = GPP - \frac{\Delta B}{1 - r_g}. \label{RM} \end{equation}
Maintenance respiration $R_m$ is further modelled proportional to the already existing aboveground biomass $B$ [$t_{ODM}$] of an individual:
\begin{equation}
R_{m} = \kappa_T \cdot r_{m} \cdot B,
\label{R_main}
\end{equation}
where $r_{m}$ denotes the maintenance respiration rate [$\frac{1}{y}$] and $\kappa_{T}$ represents a limitation factor dependent on air temperature (see section Competition and environmental limitations).
Combining the last two eqations above and arranging in terms of the respiration rate $r_m$ results in: \begin{equation} r_{m} = \frac{1}{B \cdot \kappa_T} \cdot \left(GPP - \frac{\Delta B}{1 - R_g}\right). \label{rmrate} \tag{84} \end{equation}
In FORMIND 3.0 we have two different approaches of calculating the maintenance respiration rate based on the eqn. above:
- Optimal approach (no limitation)
- Observation-based approach
In the following, we describe both approaches in greater detail.
Optimal approach (most frequently used)
The maintenance respiration rate $r_{m}$ of the eqn. above is calculated using the assumption of full resource availability. That is, it is assumed that full resource availability (i.e. no limitation by shading, soil water or air temperature) results in the observed maxima of field measurements of stem diameter increments:
\begin{equation}
r_{m} = \frac{1}{B} \cdot \left(P_{ind}(I_0) - \frac{B(D+g(D))-B}{(1-R_g)}\right),
\label{R_mainsimple}
\end{equation}
where this equation can be obtained by substituting in eqn. (\ref{rmrate}) (i) $\kappa_T$ by 1, (ii) $GPP$ by the gross productivity under full resource availability $P_{ind}(I_0)$ (see eqn. \ref{GPP_tree}) with $I_0$ as the full available incoming irradiance and (iii) $\Delta B$ by the biomass increment derived from the maximum stem diameter increment under full resource availability $D+g(D)$ using the individual's geometry (see section Geometry). See section Maximum diameter growth curve for different modelling approaches of the maximum diameter growth curve $g(D)$.
This approach is proposed when climate data at the time of field measurements are not available.
Observation-based approach
In this approach, the maintenance respiration rate $r_{m}$ is calculated including those climatic conditions, that were observed during the field measurements of stem diameter increments. The correspondence of environmental factors (see section Competition and environmental limitations) to these climatic conditions during the observations is indicated by $\check{\cdot}$.
\begin{equation}
r_{m} = \frac{1}{B} \cdot \left(GPP(\check{I_{ind}},\check{\varphi_{act}},\check{\varphi_T},\check{\varphi_W}) - \frac{B(D+g(D))-B}{(1-R_g)} \right),
\label{R_mainref}
\end{equation}
This equation can be obtained by substituting in eqn. (\ref{rmrate}) (i) $\kappa_T$ by 1, (ii) $GPP$ by the gross productivity under the climate during observations $GPP(\check{I_{ind}},\check{\varphi_{act}},\check{\varphi_T},\check{\varphi_W})$ and (iii) $\Delta B$ by the biomass increment derived from the maximum stem diameter increment using the individual's geometry $D+g(D)$ (see section Geometry). See section Maximum diameter growth curve for different modelling approaches of the maximum diameter growth curve $g(D)$.
This approach is proposed when climate data are available at the time field data on stem diameter increments were measured. In general, diameter increments are determined based on the difference of stem diameter measurements between two dates. For this time period climate data would be needed on which the limitation factors $\check{I_{ind}}$, $\check{\varphi_{act}}$, $\check{\varphi_T}$ and $\check{\varphi_W}$ of the eqn. above can be calculated as described in section Competition and environmental limitations.
Maximum diameter growth curve
In the field, diameter increments can be determined by calculating the differences between two measurements of the stem diameter per tree (at two distinct observation dates). The increments are then usually plotted against the measured stem diameter of the first observation date to get an impression of how much a tree of stem diameter $D$ is able to increase (see Fig below for an example).
Illustration of a measured diameter growth curve. Points represent illustrative measurements. The solid line represents a growth function to the maximum values of the measurements. Dotted lines show important characteristics that would be needed for the first approach.
Such point clouds as illustrated in the Fig. above can be described by functional relationships. Please note that you have to adjust the increments according to a time step of 1 year. That means, if there is a period of e.g. 5 years between both observation dates of stem diameter measurements, you would have to correct the increments with respect to the smaller time scale.
In FORMIND 3.0 we have two different approaches of determining the diameter growth function $g(D)$:
- Calculation of coefficients from curve characteristics
- Coefficients as input parameters
Below, we describe both approaches in more detail.
Calculation of coefficients from curve characteristics
Only a few information of the measured diameter increment curve need to be derived:
- maximum diameter increment $\Delta D_{max}$ [m/y]
- stem diameter $D_{\Delta D_{max}}$ [$% ~ \text{of}~ D_{max}$], which reaches $\Delta D_{max}$
- maximum diameter increment $\Delta D_{D_{min}}$ [$% ~ \text{of}~ \Delta D_{max}$] of the smallest possible tree (with $D = D_{min}$)
- maximum diameter increment $\Delta D_{D_{max}}$ [$% ~ \text{of}~ \Delta D_{max}$] of the biggest possible tree (with $D = D_{max}$)
Based on these characteristics, the coefficients of the growth function $g(D)$ can be calculated explicitly. Two different approaches are available:
- Polynomial approach
- Chanter approach
In the following, we show for both functional approaches of $g(D)$ the calculation of their coefficients.
Polynomial approach
The polynomial approach describes the growth function $g(D)$ as a third order polynomial: \begin{equation} g(D)=a_0 + a_1 \cdot D + a_2 \cdot D^2 + a_3 \cdot D^3, \label{growth} \end{equation} where $a_0$,$a_1$,$a_2$ and $a_3$ are the type-specific coefficients, which are calculated as follows: \begin{eqnarray*} a_3 &=& \frac{(x_0 \cdot x_1 + (\Delta D_{D_{min}} - \Delta D_{D_{max}}) \cdot \Delta D_{max} \cdot x_2)}{x_3+x_4+x_5+x_6+x_7}\\ a_2 &=& \frac{(x_0 - a_3 \cdot x_8)}{(2 \cdot D_{min} \cdot (D_{\Delta D_{max}} \cdot D_{max}) - (D_{\Delta D_{max}} \cdot D_{max})^2 - D_{min}^2)}\\ a_1 &=& -3 \cdot a_3 \cdot (D_{\Delta D_{max}} \cdot D_{max})^2 - 2 \cdot a_2 \cdot (D_{\Delta D_{max}} \cdot D_{max}) \\ a_0 &=& \Delta D_{D_{min}} \cdot \Delta D_{max} - a_3 \cdot D_{min}^3 - a_2 \cdot D_{min}^2 - a_1\cdot D_{min}\ \end{eqnarray*} with \begin{eqnarray*} x_0 &=& \Delta D_{max}-\Delta D_{D_{min}} \cdot \Delta D_{max}\\ x_1 &=& 2 \cdot (D_{\Delta D_{max}} \cdot D_{max}) \cdot (D_{min} - D_{max}) - D_{min}^2 + D_{max}^2\\ x_2 &=& 2 \cdot (D_{\Delta D_{max}} \cdot D_{max}) \cdot (D_{min} - (D_{\Delta D_{max}} \cdot D_{max})) - D_{min}^2 + (D_{\Delta D_{max}} \cdot D_{max})^2\\ x_3 &=& (D_{\Delta D_{max}} \cdot D_{max})^4 \cdot (D_{max} - D_{min})\\ x_4 &=& 2 \cdot (D_{\Delta D_{max}} \cdot D_{max})^3 \cdot (D_{min}^2 - D_{max}^2)\\ x_5 &=& (D_{\Delta D_{max}} \cdot D_{max})^2 \cdot (5 \cdot D_{min}^3 + 3 \cdot D_{min} \cdot D_{max}^2 - 3 \cdot D_{max} \cdot D_{min}^2 + D_{max}^3)\\ x_6 &=& 2 \cdot (D_{\Delta D_{max}} \cdot D_{max}) \cdot (D_{max} \cdot D_{min}^3 - D_{min} \cdot D_{max}^3)\\ x_7 &=& D_{max}^3 \cdot D_{min}^2 - D_{max}^2 \cdot D_{min}^3 + D_{min}^4 - D_{min}^5\\ x_8 &=& 3 \cdot D_{min} \cdot (D_{\Delta D_{max}} \cdot D_{max})^2 - 2 \cdot (D_{\Delta D_{max}} \cdot D_{max})^3 - D_{min}^3\ \ \end{eqnarray*}
Chanter approach
This approach describes the growth function $g(D)$ as follows: \begin{equation} g(D)=a_0 \cdot D \cdot \left(1 - \frac{D}{D_{max}}\right) \cdot e^{-a_1 \cdot D}, \end{equation} where $a_0$ and $a_1$ are the type-specific coefficients, which are calculated by: \begin{eqnarray*} a_0 &=& \frac{e^{\frac{D_{max} - 2 \cdot (D_{\Delta D_{max}} \cdot D_{max})}{D_{max} - (D_{\Delta D_{max}} \cdot D_{max})}} \cdot D_{max} \cdot \Delta D_{max}}{(D_{max} - (D_{\Delta D_{max}} \cdot D_{max})) \cdot (D_{\Delta D_{max}} \cdot D_{max})}\\ a_1 &=& \frac{D_{max} - 2 \cdot (D_{\Delta D_{max}} \cdot D_{max})}{D_{max} \cdot (D_{\Delta D_{max}} \cdot D_{max}) - (D_{\Delta D_{max}} \cdot D_{max})^2},\\ \end{eqnarray*} where $D_{max}$ is calculated out of maximum height (see section Maximum Values).
Coefficients as input parameter
For this approach, the coefficients of the corresponding growth function $g(D)$ are input parameter already known prior to the start of the simulation. The following three different functional approaches of $g(D)$ are implemented:
Weibull approach
The growth function $g(D)$ is described by a Weibull function of: \begin{equation} g(D) = a_0 \cdot a_1 \cdot a_2 \cdot (a_1 \cdot D)^{a_2 - 1} \cdot e^{-(a_1 \cdot D)^{a_2}}, \end{equation} where $a_0$, $a_1$ and $a_2$ are the type-specific coefficients.
Richards approach
The growth function $g(D)$ is described by: \begin{equation} g(D) = a_0 \cdot a_1 \cdot a_2 \cdot e^{-a_1 \cdot D} \cdot \left(1 - e^{-a_1 \cdot D}\right)^{a_2 - 1}, \end{equation} where $a_0$, $a_1$ and $a_2$ are the type-specific coefficients.
Chanter approach (most freqeuntly used)
The growth function $g(D)$ is described by: \begin{equation} g(D) = a_0 \cdot D \cdot \left(1 - \frac{D}{D_{max}}\right) \cdot e^{-a_1 \cdot D}, \end{equation} where $a_0$ and $a_1$ are the type-specific coefficients.
Please note, when determining the type-specific coefficients prior to the start of the simulation, that the curve represents growth under full resource availability. That means, not all measurements should be fitted, but only the maximum diameter increments (see Fischer 2010 p. 55 for an example).
Disturbance
Disturbances comprise the following scenarios:
- fire events, which affect trees depending on their fire resistance
- landslide events, which create bare soil
In total, $N_D$ individuals of a cohort are dying due to disturbance induced mortality events.
Fire
The fire module in FORMIND is published in Fischer 2021. Fire is the primary disturbance process affecting the terrestrial biosphere (Pfeiffer et al. 2013). Especially wildfires affect species composition and vegetation structure in forests. They lead to a decrease of carbon storage and result in the emission of greenhouse gases. There is a long tradition in fire ecology to understand these processes and their interactions. Numerous methods were developed to estimate the disturbances due to fire events. Fire events are a complex distubances, which can be described by fire frequency, fire area and severity.
To understand the effect of fire on vegetation dynamics and vegetation structure, we developed the forest fire module ForFire, which is a combination of the ideas of wellestablished fire models (Gardner et al. 1999 Keane et al. 2004 Thonicke et al. 2001). External inputs to the ForFire module are the mean fire frequency per hectare and year ($\lambda$ in $[years]$), the mean fire size related to the investigated forest area ($\beta$ in $[\%]$) and the mean fire severity ($s_{fire}$ $[0-1]$). Fire events are implemented on the patch level, i.e. the smallest possible fire size has the size of one patch ($A_{patch}$), the biggest are considered are all patches of the simulation area.
- fire events: We implemented fire events in the following way: in every year a random number determines the number of fire events within this year. This fire frequency is poisson distributed (Green 1989) with $\lambda$ as mean time between fire events. If a fire event occurs, the fire centre is chosen randomly within the simulated forest area. The fire size (equal to the number of burned patches) is described by an exponential distribution $\beta$ as mean size of the fire area related to the whole simulated forest area (Green 1989). The fire spread is modelled randomly: (i.) going from the fire centre every neighboring patch is burned, (ii.) a randomly burned patch is chosen and (iii.) again every neighboring patch is burned. This procedure is repeated until the number of the burned patches is equal to the specified fire size.
 Figure 11: Visualization of two randomly chosen fire events. The simulated area is nine hectare. The grey level indicates the amount of standing biomass. The red colour shows the fire spread.
Figure 11: Visualization of two randomly chosen fire events. The simulated area is nine hectare. The grey level indicates the amount of standing biomass. The red colour shows the fire spread.
- fire tolerance of trees: According to the fire tolerance of a tree species, not every tree is burning and dying in the fire area. The probability for tree burning depends on fire tolerance of the species, on the stem diameter ($D$ $[cm]$) as a proxy of tree age and on the fire severity (Busing & Solomon 2006). We distinguish between four fire tolerance levels for tree species. Tree species of level 1 are dying in a fire, independent of stem diameter or fire severity. Tree species with a fire tolerance up to level 4 have an increasing fire-resistance. The burning probability for every tree is calculated as follows depending on the fire tolerance of the tree species (Busing & Solomon 2006):
\begin{align}
P_{F1} &= 1 \\ P_{F2} &= e^{((-(1-s_{fire}) \cdot 0.00202)-0.00053) \cdot D} \\ P_{F3} &= e^{((-(1-s_{fire}) \cdot 0.02745)-0.00255) \cdot D} \\ P_{F4} &= e^{-0.00053 \cdot D} - 0.5 - (1 - s_{fire}) \cdot 0.5 \end{align} where $s_{fire}$ (value between $0-1$) is an indicator for the severity and the type of the fire (see figure below) and $D$ is the stem diameter.
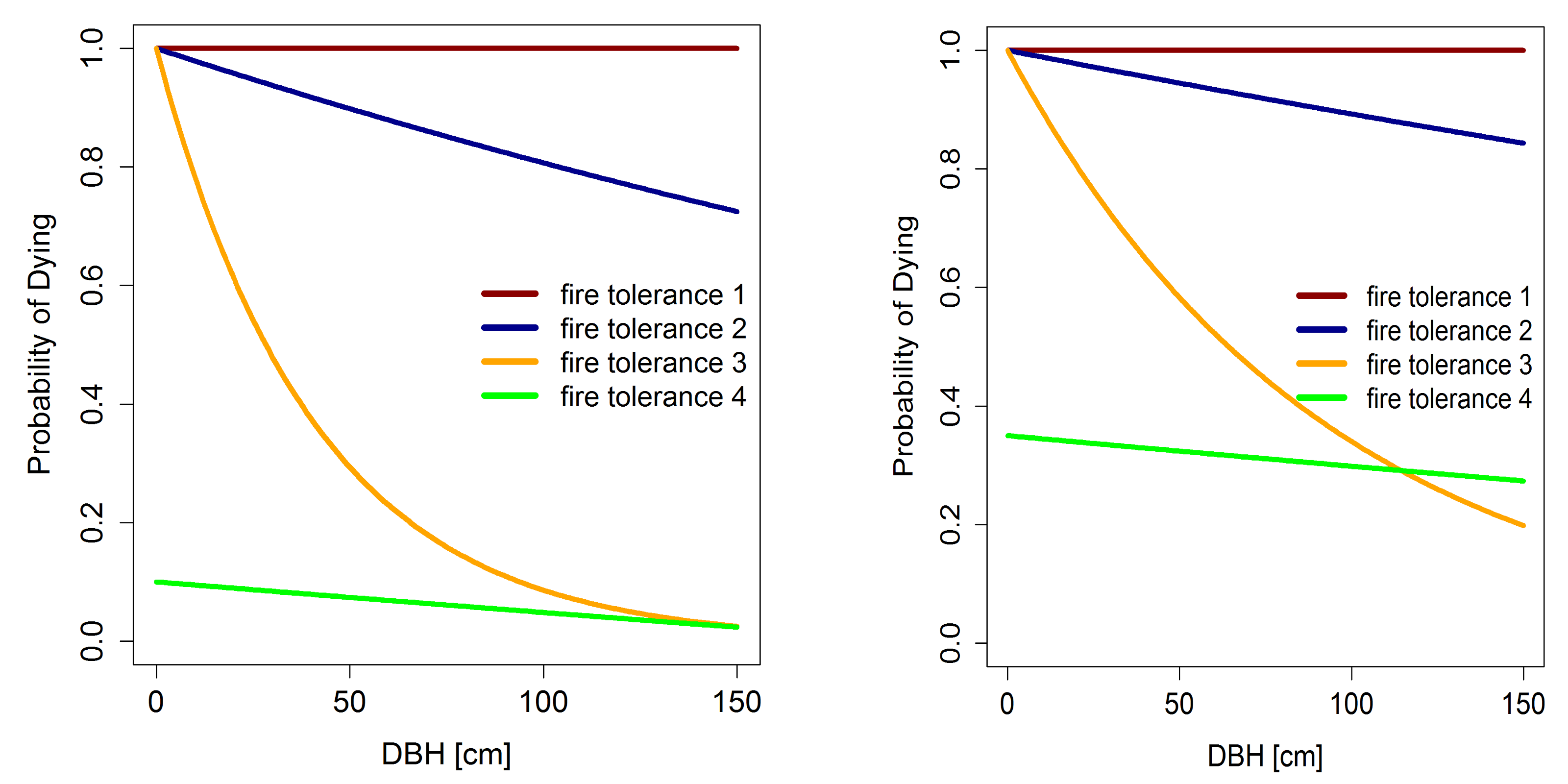 Figure 12: Probability for tree dying after a fire event depending on stem diameter ($D$) and fire tolerance group. Left: probability of dying after a weak fire event ($s_{fire} = 0.2$). Right: probability of dying after a strong fire event ($s_{fire} = 0.7$).
Figure 12: Probability for tree dying after a fire event depending on stem diameter ($D$) and fire tolerance group. Left: probability of dying after a weak fire event ($s_{fire} = 0.2$). Right: probability of dying after a strong fire event ($s_{fire} = 0.7$).
Landslides
In montane forests shallow landslides can constitute a recurring natural disturbance. Disturbance by landslides differs from disturbances by falling trees or logging in the sense that all vegetation, as well as upper soil layers and seed bank are removed from the disturbed patch. Forest regeneration on landslide surfaces therefore underlies particular environmental conditions. For instance, solar radiation on recent landslide sites is high and nutrient levels of landslide soils are low (Wilcke et al. 2003). Due to this changed environmental conditions, establishment rates of trees as well as tree mortality and tree growth rates might deviate from the basic type-specific rates.
To study potential effects of landslide disturbances on the forest carbon cycle and species composition, we implemented landslides as a particular type of disturbance into the FORMIND 3.0 model. External inputs to the landslide module are the landslide frequency per hectare and year ($slidefreq$) and the distribution of landslide sizes. Landslide disturbance is implemented on the patch level, i.e. the smallest possible landslide has the size of one patch $A_{patch}$ (i.e. 20 m x 20 m) and the biggest landslides considered are for example 25 patches (1 hectare).
We implemented landslides in the following way: for each hectare and in every year a randomly drawn number determines whether a landslide occurs (probability $f_{land}$). Since the annual frequency on a per hectare basis will usually be small, we do not account for multiple landslides on one hectare in the same year. The size of the landslide is drawn from a size distribution ($s$) of landslides, rounded for the patch size $A_{patch}$. The starting location of the landslide is a random patch and the directionality of landslides is always the same. Neighbouring patches of the starting location are affected until the slide reaches the predetermined size. All trees in landslide affected patches die and are removed from the patch. Since recruiting trees in FORMIND 3.0 have a stem diameter of $D_{min}$ $[cm]$ at breast height, there is a time lag ($t_{lag}$) between the landslide event and the occurrence of the first trees on the slide surface. Based on the potential growth of trees this time lag can be estimated for the different tree types. Forest recovery then proceeds according to one of the following scenarios: undisturbed regrowth, reduced growth, reduced recruitment, increased mortality. For the justification of these scenarios, see Dislich & Huth 2012.
- Undisturbed regrowth: All type-specific parameters stay unchanged. This situation considers increased light levels after the landslide disturbance but neglects additional environmental changes.
All other scenarios describe a temporal change in type-specific traits. The underlying assumption is that the strongest change in traits occurs immediately after the landslide and traits come back to their normal level, as forest recovery proceeds after the disturbance. The parameter $r_{land}$ represents the assumed change in tree species attributes after landslide occurrence.
-
Reduced growth: FORMIND 3.0 calculates tree growth as biomass increment per year ($\Delta B$, cf. section F.3). Assuming a simple linear relation between growth reduction and "recovery status" of the disturbed site, which is expressed by the ratio of accumulated dead biomass ($B_{dead}$) to the minimum biomass in a mature patch ($B_{mat}$), the reduced biomass increment ($\Delta B_{red}$) is calculated via: \begin{align} \Delta B_{red}(B_{dead}) &= \left( r_{land} \cdot \frac{B_{dead}}{B_{mat}} + (1 - r_{land}) \right) \cdot \Delta B \end{align}
-
Reduced recruitment: The type-specific recruitment rate per hectare and year ($N_{seed}$, cf. section C) might be changed due to landslide disturbances. Like in the reduced growth scenario, we assume a linear relationship between the amount of recruitment reduction and recovery status of the patch, now expressed by the ratio of established biomass in the recovering patch ($B_{pat}$) to the minimum biomass of a mature patch ($B_{mat}$). Therefore the reduced recruitment rate ($N_{red}$) is calculated via: \begin{align} N_{red}(B_{dead}) &= \left( r_{land} \cdot \frac{B_{pat}}{B_{mat}} + (1 - r_{land}) \right) \cdot N_{seed} \end{align}
-
Increased mortality: The type-specific mortality rate ($M$) might change due to landslide disturbance (cf. section D). Again, we assume a linear relationship between the increment in mortality rate and the recovery status of the patch, represented by the ratio of established biomass in the recovering patch ($B_{pat}$) to the minimum biomass of a mature patch ($B_{mat}$). Therefore the increased mortality rate ($M_{inc}$) is calculated as: \begin{align} M_{inc}(B_{pat}) = \left( 1 + \left( r_{land} - r_{land} \cdot \frac{b_{pat}}{B_{mat}} \right) \right) \cdot M \end{align}
The choice of the parameter $r_{land}$ as well as the chosen functional relationship between changed attributes and recovery state of the successional forest is adapted according to site specific knowledge. Exemplary values for the parameters $t_{lag}$, $r_{land}$ and $f_{land}$, as well as the slide size distribution, are shown in the tables below.
Table 4: Exemplary values for the time lag parameter $t_{lag}$ (Dislich & Huth 2012).
| Type | $t_{lag}$ |
|---|---|
| pioneer species | 3 |
| mid-successional species | 5 |
| climax species | 12 |
Table 5: Exemplary values for the parameters $r_{land}$ and $f_{land}$ (Dislich & Huth 2012).
| Parameter | Value |
|---|---|
| $r_{land}$ | 0.9, 0.5 |
| $f_{land}$ | 0.02 |
Table 6: Exemplary slide size distribution $s$ (Dislich & Huth 2012).
| Landslide size [$m^2$] | Frequency |
|---|---|
| 400 | 0.30 |
| 800 | 0.26 |
| 1200 | 0.16 |
| 1600 | 0.09 |
| 2000 | 0.08 |
| 2400 | 0.03 |
| 2800 | 0.03 |
| 3200 | 0.01 |
| 3600 | 0.03 |
| 4000 | 0.005 |
| 4400 | 0.005 |
| $\geq$ 4800 | 0 |
Carbon cycle
Modelling the forest carbon cycle
The calculation of the carbon cycle in FORMIND 3.0 uses a simple compartment approach consisting of the following explicit carbon stocks:
- living forest stock, which equals the amount of carbon of alive trees
- deadwood stock $S_{\text{dead}}$, which equals the amount of carbon of dead trees
- slow decomposing soil stock $S_{\text{slow}}$, which accounts for the slow decomposing share of carbon in the deadwood stock
- fast decomposing soil stock $S_{\text{fast}}$, which accounts for the fast decomposing share of carbon in the deadwood stock
Schematic visualization of the carbon cycle in FORMIND 3.0. Circles represent explicit carbon stocks and the rectangle indicates the atmosphere. Dotted arrows show carbon released to the atmosphere from the respective stock and block arrows show carbon transitions between the respective explicit carbon stocks.
The dynamics of the living forest stock (i.e. carbon storage in form of growth and carbon releases as respiration) are described earlier in section Growth of a tree. The dynamics of the remaining stocks is described by a set of differential equations:
\begin{align} \frac{\mathrm{d} S_{dead}}{\mathrm{d} t} &= S_{\text{mort}} - (t_{S_{\text{dead}}\rightarrow A} + t_{S_{\text{dead}}\rightarrow S_{\text{slow}}} + t_{S_{\text{dead}}\rightarrow S_{\text{fast}}}) \cdot S_{\text{dead}} \\ \frac{\mathrm{d} S_{\text{slow}}}{\mathrm{d} t} &= t_{S_{\text{dead}}\rightarrow S_{\text{slow}}}\cdot S_{\text{dead}}-t_{S_{\text{slow} \rightarrow A}}\cdot S_{\text{slow}} \\ \frac{\mathrm{d} S_{\text{fast}}}{\mathrm{d} t} &= t_{S_{\text{dead}} \rightarrow S_{\text{fast}}}\cdot S_{\text{dead}}-t_{S_{\text{fast} \rightarrow A}}\cdot S_{\text{fast}} \end{align}
where the parameters $t_{S_{\text{dead}}\rightarrow A}$, $t_{S_{\text{slow}}\rightarrow A}$ and $t_{S_{\text{fast}} \rightarrow A}$ denote transition rates in $\tfrac{1}{\text{yr}}$ of released carbon from the respective soil stocks to the atmosphere. The parameter $t_{S_{\text{dead}} \rightarrow S_{\text{slow}}}$ and $t_{S_{\text{dead}} \rightarrow S_{\text{fast}}}$ represent in turn decomposition rates of deadwood material in $\tfrac{1}{\text{yr}}$. The variable $S_{\text{mort}} \left[\tfrac{\text{t}_\text{C}}{\text{ha}} \right]$ represents the carbon of all trees dying within the current time step (see section Mortality).
Determining the transition rates
The transition rates depend on how fast microorganisms can decompose the fallen litter or dead trees. For describing the decomposition rates, we use an approach presented earlier by Sato et al. 2007. The annual decomposition rate $t_{s_{\text{dead}}}$ for the deadwood stock is calculated as follows:
\begin{equation} t_{S_{\text{dead}} }=\text{min}\left( 1.0,\frac{10^{-1.4553+0.0014175\cdot AET}}{12} \right) \end{equation}
where $AET$ is considered as the actual evapotranspiration in the previous year in mm. The variable $AET$ is calculated by the sum of interception $IN$ and transpiration $TR$ (cf. section Water cycle and soil water limitation).
The annual decomposition rate $t_{s_{\text{dead}} }$ is modelled as the sum of all transitions rates of the deadwood pool $S_{\text{dead}}$:
\begin{equation} t_{S_{\text{dead} }}=t_{S_{\text{dead}} \rightarrow A}+t_{S_{\text{dead} } \rightarrow S_{\text{slow}}}+t_{S_{\text{dead}} \rightarrow S_{\text{fast}}} \end{equation}
According to Sato et al. 2007 70 % of the carbon of decomposing deadwood biomass (i.e. litter) is directly released to the atmosphere, while the remaining 30 % are transferred to the slow and fast decomposing soil stocks. In detail, 98.5 % of the remaining carbon is transferred to the fast soil stock and 1.5 % to the slow soil stock. We then calculate the specific transition rates as follows:
\begin{align} t_{S_{\text{dead} }\rightarrow A} &= 0.7\cdot t_{S_{\text{dead}} } \\ t_{S_{\text{dead} }\rightarrow S_{\text{slow}}} &= 0.015\cdot 0.3\cdot t_{S_{\text{dead}} } \\ t_{S_{\text{dead} }\rightarrow S_{\text{fast}}} &= 0.985\cdot 0.3\cdot t_{S_{\text{dead}} } \end{align}
The Net Ecosystem Exchange (NEE)
The NEE is the carbon net flux of the forest. We define the $NEE \left[ \tfrac{\text{t}_\text{C}}{\text{ha yr}} \right]$ as follows:
\begin{equation} NEE = C_{GPP}-C_{R}-t_{S_{\text{dead}}\rightarrow A}\cdot S_{\text{dead}}-t_{S_{\text{slow}}\rightarrow A}\cdot S_{\text{slow}}-t_{S_{\text{fast}}\rightarrow A}\cdot S_{\text{fast}} \end{equation}
where $S_\text{dead} \left[ \tfrac{ \text{t}\text{C}}{\text{ha}} \right]$ denotes the deadwood carbon pool, $S{\text{slow}} \left[\tfrac{\text{t}\text{C}}{\text{ha}} \right]$ and $S{\text{fast}} \left[\tfrac{\text{t}\text{C}}{\text{ha}} \right]$ the soil carbon stock (i.e. slow and fast decomposing), $t{x \rightarrow A} \left[ \tfrac{1}{\text{yr}} \right]$ the corresponding transition rates of released carbon from the respective stock $x$ resulting from the microbiological respiration (cf. section Carbon cylcle) and $C_{GPP} \left[\tfrac{\text{t}\text{C}}{\text{ha yr}} \right]$ is the carbon captured in the gross primary productivity of the living forest (cf. section Gross primary production), $C_R \left[\tfrac{\text{t}\text{C}}{\text{ha yr}} \right]$ is the carbon released by the total respiration of the living forest (i.e. for maintenance and growth). We also assume here that $1 \text{g}$ organic dry matter contains 44 % carbon, which results in:
\begin{align} C_{GPP} &= 0.44\cdot \sum_{\text{all trees}}^{} GPP \\ C_{R} &= 0.44 \cdot \sum_{\text{all trees}}^{} (R_{m}+R_{g}\cdot (GPP-R_{m})) \end{align}
If the $NEE$ is positive (i.e. $NEE > 0 $), the forest is considered to be a carbon sink. If the $NEE$ is negative (i.e. $NEE < 0$), the forest is considered to be a carbon source.
Logging
Commercial trees are logged on selected areas. Trees with specific attributes are removed from the forest plot. At the same time, surrounding trees are damaged based on the chosen logging strategy, logging intensity, logging cycle, cutting limits and resulting damage Huth et al. 2005.
Logging strategy
The two logging strategies that are provided in
FORMIND, arise from different commercial and economical interests. The
two strategies differ in the falling direction of a logged tree:
The reduced impact logging (RIL) takes into account a substantial
planning of the logging scenario. This scenario is implemented into
FORMIND by defining the falling direction of a tree towards the biggest
gap. Thereby, the falling tree causes a reduced amount of damage to
surrounding trees. The conventional logging (CON) takes into account the usage of heavy
machinery, unskilled workers and low to no planing strategies. This is
implemented into FORMIND by a random falling direction of logged trees.
The random direction causes the possibility of higher damage to
surrounding trees.
Logging intensity
The logging intensity is defined by the minimum number of trees harvested within the forest plot $L_\text{N min} \, [\text{-}]$ and the maximum number of trees $L_\text{N max} \, [\text{-}]$.
Logging cycle
The first logging scenario is defined as $L_\text{start} \, [\text{y}]$. The logging cycle is the time between logging events $L_\text{C} \, [\text{y}]$.
Cutting limit
Commercial trees are are only logged if their stem diameter $D\, [\text{m}]$ exceed a minimum stem diameter $L_\text{D min} \, [\text{m}]$.
logging intensity
Logging intensity is defined as the number of remaining commercial trees in the forest after the logging event $L_\text{remain} \, [\text{-}]$.
Damage
The induced damage to surrounding trees depends on the stem diameter $D\, [\text{m}]$ of the logged tree - bigger trees cause more damage to surrounding trees than smaller trees. Therefore, a percental damange $L_\text{damage} \, [\text{-}]$ is defined for four different diameter classes $L_\text{dbhClass} \, [\text{-}]$.
Lidar simulation
FORMIND allows the simulation of a Lidar scan of the forest stand at each time step (Knapp et al. 2018). The Lidar simulator generates point clouds of discrete returns as they are usually produced by small-footprint Lidar systems.
Entities, state variables and scales
The basic entities in the model are trees, Lidar pulses and Lidar returns. Trees are characterized by their position (X- and Y-coordinate), height, crown length, crown radius and crown shape (spheroid, cone or cylinder). Modeled Lidar pulses are all perfectly vertical with regular spacing between them. Thus a Lidar pulse is only characterized by its X- and Y-coordinate. Lidar returns are points in 3 dimensional space, characterized by their X-, Y- and Z-coordinate. The model works in a 3D space represented by an array of cubic voxels of a certain side length. The resolution is determined by the voxel side length, which can be chosen according to the desired spacing of Lidar pulses, as each pulse is simply represented by one vertical column of voxels.
Process overview and scheduling
In the model at first a voxel representation of the entire forest is created. This means the value of each voxel in the 3D array that falls into a tree crown or trunk of any given tree in the input list is set to one (tree voxel). All other voxels, representing free space that is not occupied by trees get the value zero, except for the forest floor (Z = 0), where each voxel gets the value one. Whether a voxel becomes a tree voxel or not depends on the tree parameters position, height, crown dimensions and shape. Precise tree positions within each 20 m x 20 m patch are assigned randomly but consistent with other FORMIND outputs, e.g. the stand visualization file. The voxel forest is hereafter scanned with a virtual Lidar. Each vertical column of voxels is considered one Lidar pulse, which can cause multiple returns. The returns are collected for each X-Y-coordinate-combination in the array.
Design concepts
The Lidar simulation follows a probabilistic approach. Instead of explicitly simulating the branches and foliage and their interaction with laser beams within the tree crowns, the model assumes that the tree crown space is a homogeneous, turbid medium. The probability to get a Lidar return from a certain point decreases with increasing distance that the laser beam has to travel through the medium before reaching that point. This is analogous to the light-extinction law after Lambert-Beer, which is also used for the light climate simulation. The only difference is that the classical Lambert-Beer equation serves to calculate remaining light intensity depending on distance, while in the discrete Lidar case the same equation is used to calculate probability $P_\text{Lid}$ for a discrete return here.
\begin{equation} P_{Lid}(d_{Lid}) = P_{0, Lid} \cdot e^{-k_{Lid} \cdot d_{Lid}} \end{equation}
Returns can only exist in tree and ground voxels. Distance $d_\text{Lid}$ that the beam has to travel through crown space before reaching a focal voxel is quantified from the count of tree voxels above the focal voxel in the same array column. $P_{0, Lid}$ represents the probability to get a return from the very upper voxel, where the laser beam hits the surface (tree or ground) for the first time. The parameter $k_{Lid}$ is the exponential extinction coefficient, which determines how fast the return probability decreases after entering the crown space. The final decision for each voxel whether it will contain a return or not is taken stochastically, based on the calculated return probability. Model outputs are tables that contain the coordinates of all tree voxels and all Lidar returns. Parameters $P_{0, Lid}$ and $k_{Lid}$ can be set independently for vegetation ($P_{0, Lid, V}$, $k_{Lid, V}$) and ground ($P_{0, Lid, G}$, $k_{Lid, G}$) voxels to adapt to the different reflectance of the forest floor. Further parameters to run the FORMIND Lidar simulator are the pulse spacing $s_{Lid}$ and the time interval between successive scans $t_{Lid}$. The Lidar simulation works with periodic boundaries, meaning that tree crowns protruding the limits of the simulated area on one side reappear on the opposite side.
Figure: Schematic visualization of the Lidar model. On the left side a forest stand of 1 ha is shown. In the center
you see a voxel representation of the stand with colors indicating Lidar
return probability from high (red) to low (blue) for each voxel. On the
right side the final simulated point cloud is shown with colors
indicating height above ground from 0 m (blue) to 40 m (orange).
Input parameters and variables
The following parameters are not properly named and will be renamed
| Old name | New name |
|---|---|
| TimeEnd | timeEnd |
| TimeStep | timeStep |
| switches.Ha | switches.sideLengthOfSimulationArea |
| par.seedDispersalKernelShapeParams | par.seedDispersalMaxDistance |
| par.seedDispersalKernelLocationParams | par.seedDispersalAverageDistance |
Table 7: Parameters of the simulation.
| General Input Parameters of Simulation | |||
|---|---|---|---|
| Symbol | Description | Unit | Source Code Variable |
| $A_{\text{area}}$ | side length of simulated area | $\text{m}$ | switches.sideLengthOfSimulationArea |
| $A_{\text{patch}}$ | patch area | $\text{m}^{2}$ | |
| $n_{\text{patches}}$ | number of patches per simulation area | $-$ | |
| $t_{y}$ | length of simulation | $\text{yr}$ | timeEnd |
| $Δt$ | time step | $\text{yr}$ | timeStep |
| number of species groups (PFTs) | $-$ | par.pftCount | |
| Geometric Input Parameters | |||
| Symbol | Description | Unit | Source Code Variable |
| mathematical form of the allometric relationships | $-$ | par.allometricRelationships | |
| $h_{0}, h_{1}, h_{2}$ | coefficients of height-stem diameter relationship | $-$ | par.heightFromDbhParams |
| $c_{l0}, c_{l1}, c_{l2}$ | coefficients of crown-length-height relationship | $-$ | par.crownLengthFactorFromHeightParams |
| $c_{d0}, c_{d1}, c_{d2}, c_{d3}$ | coefficients of crown-diameter-stem-diameter relationship | $-$ | par.crownDiameterFromDbhParams |
| $ρ$ | wood density | $\frac{\text{t}_{\text{ODM}}}{\text{m}^3}$ | par.woodDensities |
| $σ$ | ratio of total aboveground biomass to stem biomass | $-$ | par.stemBiomassFractionParams |
| $f$ | form factor | $-$ | |
| $f_{0}, f_{1}, f_{2}$ | coefficients of form-factor-stem-diameter relationship | $-$ | par.formFactorFromDbhParams |
| $b_{0}, b_{1}, b_{2}$ | coefficients of biomass-stem-diameter relationship | $-$ | par.biomassFromDbhParams |
| $l_{0}, l_{1}$ | LAI-stem-diameter relationship | $-$ | par.laiFromDbhParams |
| $D_{\text{max}}$ | maximal stem diameter | $\text{m}$ | par.maxPlantSizes |
| $H_{\text{max}}$ | maximal height | $\text{m}$ | par.maxPlantSizes |
| $B_{\text{max}}$ | maximal aboveground biomass | $\text{t}_{\text{ODM}}$ | |
| Recruitment and Establishment Input Parameter | |||
| Symbol | Description | Unit | Source Code Variable |
| $N_{\text{seed}}$ | global in-growth rate of seeds | $\frac{1}{\text{ha yr}}$ | par.externalSeedInfluxPerHectare |
| $N_{\text{init}}$ | initial seed number in seed pool | $\frac{1}{\text{patch}}$ | |
| $D_{\text{rep}}$ | minimum stem diameter of a seed producing mother tree | $\text{m}$ | par.minSeedProductionDbhs |
| $f_{\text{disp}}$ | dispersal kernel | $-$ | par.dispersalKernelFunctions |
| $dist_{\text{mean}}$ | average dispersal distance | $\text{m}$ | par.seedDispersalAverageDistance |
| $dist_{\text{max}}$ | maximum dispersal distance | $\text{m}$ | par.seedDispersalMaxDistance |
| $σ$ | ratio of total aboveground biomass to stem biomass | $-$ | |
| $I_{\text{seed}}$ | percentage of incoming radiation at floor required for germination | $%$ | par.minEstablishmentIrradianceFraction |
| $M_{\text{pool}}$ | mortality rate of seeds in the seed pool | $\frac{1}{\text{yr}}$ | par.seedPoolMortalityRates |
| $max_{\text{dens}}$ | maximal number of germinating seedlings | $\frac{1}{\text{patch}}$ | par.maxSeedlingsPerPatch |
| $D_{\text{min}}$ | initial stem diameter of a germinated seedling | $\text{m}$ | par.seedlingDbh |
| Mortality Input Parameters | |||
| Symbol | Description | Unit | Source Code Variable |
| mathematical form of death rate computation | par.mortalityFunction | ||
| $M_{B}$ | base / background mortality rate | $\frac{1}{\text{yr}}$ | par.backgroundMortalityParams |
| $m_{d0}, m_{d1}$ | mortality rate dependent on stem diameter | $-$ | par.mortalityFromDbhParams |
| $m_{i0}, m_{i1}, m_{i2}$ | mortality rate dependent on stem diameter increment | $-$ | par.mortalityFromDbhIncrementParams |
| $f_{\text{fall}}$ | probability for a dead tree to fall | $-$ | par.treeFallProbability |
| Light Climate and Photosynthesis Input Parameters and Variables | |||
| Symbol | Description | Unit | Source Code Variable |
| $Δh$ | width of layers of aboveground vertical space discretization in a patch | $\text{m}$ | |
| $n_{\text{layer}}$ | number of layer of aboveground vertical space discretization | $-$ | |
| $I_{0}$ | incoming irradiance on top of canopy | $\frac{\mu\text{mol}_{\text{photon}}}{\text{m}^2 s}$ | |
| $k$ | light extinction coefficient | $-$ | par.lightExtinctionCoefficients |
| $α$ | initial slope of light response curve | $\frac{\mu\text{mol}_{\text{CO}2}}{\mu\text{mol}{\text{photon}}}$ | par.initialLightResponseSlope |
| $p_{\text{max}}$ | maximal leaf gross photosynthetic rate | $\frac{\mu\text{mol}_{\text{CO}_2}}{\text{m}^2 \text{s}}$ | par.maxGrossLeafPhotosynthesisRate |
| $m$ | transmission coefficient | $-$ | par.lightTransmissionCoefficient |
| $l_{\text{day}}$ | day length | $\text{h}$ | par.dayLength |
| $φ_{\text{ODM}}$ | conversion factor | $\frac{\text{t}{\text{ODM}}}{\mu\text{mol}{\text{CO}_2}}$ | |
| Water Module Input Parameter and Variables | |||
| ------------------------------------------------ | ----------- | --------- | -------------------- |
| Symbol | Description | Unit | Source Code Variable |
| $PR$ | precipitation | $\frac{\text{mm}}{\text{h}}$ | precipitation |
| $K_{L}$ | interception constant | $\frac{\text{mm}}{\text{h}}$ | par.Water_KL |
| $POR$ | soil porosity | $\frac{\text{mm}}{\text{h}}$ | par.Water_POR |
| $K_{s}$ | fully saturated conductivity | $\frac{\text{mm}}{\text{h}}$ | par.Water_KS |
| $Θ_{\text{res}}$ | residual soil water content | $\frac{\text{mm}}{\text{h}}$ | par.Water_SW_RES |
| $λ$ | pore size distribution index | $-$ | par.Water_L |
| $WUE$ | water-use-efficiency | $\frac{t_{\text{ODM}}}{\text{kg}_{\text{H}_2\text{O}}}$ | par.Water_WUE |
| $PET$ | potential evapotranspiration | $\frac{\text{mm}}{\text{h}}$ | |
| $Θ_{soil}^{init}$ | initial soil water content at start of simulation | $V%$ | par.InitSoilWaterContent |
| $Θ_{pwp}$ | permanent wilting point | $V%$ | par.Water_PWP |
| $Θ_{fc}$ | field capacity | $V%$ | par.Water_FC |
| $Θ_{msw}$ | minimum soil water content | $V%$ | msw |
| Temperature Input Parameter and Variables | |||
| Symbol | Description | Unit | Source Code Variable |
| $T$ | air temperature | $^\circ\text{C}$ | |
| $n$ | number of days per time step $\Delta t$ | $-$ | |
| $T_{\text{crit}}$ | critical temperature for bud-burst | $^\circ\text{C}$ | |
| $k_{0}, k_{1}, k_{2}$ | parameter of inhibition factors | $-$ | |
| $T_{\text{CO}2, l}, T{\text{CO}_2, h}$ | temperature limits of $\text{CO}_2$ assimilation | $^\circ\text{C}$ | |
| $T_{\text{hot}}, T_{\text{cold}}$ | monthly mean temperature of warmest and coldest month an individual can cope with | $^\circ\text{C}$ | par.Temperature_month_hot, par.Temperature_month_cold |
| $T_{\text{ref}}$ | reference temperature | $^\circ\text{C}$ | par.Temperature_reference |
| $Q_{10}$ | base of Q$_{10}$ function | $-$ | |
| Respiration Input Parameter and Variables | |||
| Symbol | Description | Unit | Source Code Variable |
| $R_{g}$ | growth respiration factor | $-$ | par.growthRespirationFraction |
| $g(D)$ | maximal stem diameter increment (growth) function | $-$ | |
| $a_{0}, a_{1}, a_{2}, a_{3}$ | coefficients of the growth function $g(D)$ | $-$ | |
| $x_{i}, i = 1, ..., 8$ | auxiliary variables | $-$ | |
| $ΔD_{\text{max}}$ | maximal measured stem diameter increment | $\frac{\text{m}}{\text{yr}}$ | |
| $D_{ΔD_{\text{max}}}$ | stem diameter at which maximal increment is measured | proportion of $D_{\text{max}}$ | |
| $ΔD_{D_{\text{max}}}$ | max. measured stem diameter increment for diameter $D_{\text{min}}$ | proportion of $ΔD_{\text{max}}$ | |
| $ΔD_{D_{\text{max}}}$ | max. measured stem diameter increment for diameter $D_{\text{max}}$ | proportion of $ΔD_{\text{max}}$ | |
| mean irradiance in simple climate (wet and dry) | par.meanIrradiance | ||
| $\check{I}_{\text{ind}}$ | reference for advanced irradiance | $\frac{\mu \text{mol}_{\text{photon}}}{\text{m}^2 \text{s}}$ | par.referenceIrradiance |
| $\check{\varphi}_{\text{act}}$ | reference vegetation period of parameterization climate | $\text{d}$ | |
| $\check{\varphi}_T$ | reference temperature limitation factor of photosynthesis of parameterization climate | $-$ | |
| Lidar Input Parameter and Variables | |||
| Symbol | Description | Unit | Source Code Variable |
| $P_{0,\text{Lid}, \text{V}}$ | surface return probability for vegetation voxels | $-$ | par.VegetationSurfaceReturnProbability |
| $k_{\text{Lid}, \text{V}}$ | Lidar extinction coefficient for vegetation voxels | $-$ | par.VegetationExtinctionCoef |
| $P_{0,\text{Lid}, \text{G}}$ | surface return probability for ground voxels | $-$ | par.GroundSurfaceReturnProbability |
| $k_{\text{Lid}, \text{G}}$ | Lidar extinction coefficient for ground voxels | $-$ | |
| $s_{\text{Lid}}$ | spacing between Lidar pulses | $\text{m}$ | par.PulseDistance |
| $t_{\text{Lid}}$ | time interval between Lidar scans | $\text{yr}$ | par.LidarOutputStart, par.LidarOutputStep |
Table 8: Parameters that are not listed in the handbook yet and a probable clustering
| Name | Type | Unit | Description | Parameter File |
|---|---|---|---|---|
| Model Structure | ||||
| ProjectName | string | project name shown in GUI | Argentina | |
| Carbon Dynamics | ||||
| par.CPool_DeadWood | float | t | Initial carbon content in the deadwood carbon pool | generalAmazonianForest_3pft |
| par.CPool_Soil_fast | float | t | Initial carbon content in the fast decomposing soil carbon pool | generalAmazonianForest_3pft |
| par.CPool_Soil_slow | float | t | Initial carbon content in the slow decomposing soil carbon pool | generalAmazonianForest_3pft |
| par.Cflux_aet | float | mm | Mean actual evapotranspiration (AET) | Argentina |
| Plant Growth and Physiology | ||||
| par.CrownGeometry | array | Geometrical shape of the plant crown: 1=spheroid (ellipsoid), 2=conical, 3=cylindrical | generalAmazonianForest_3pft | |
| par.HeightExpLambda | float | ForestFactory | lamdba in exponential distribution | virtual |
| par.HMax | float | ForestFactory | maxmimum height of trees | generalAmazonianForest_3pft |
| par.HMin | float | ForestFactory | minimum height of trees | generalAmazonianForest_3pft |
| par.InitialGreenFraction | float | Initial fraction of green biomass on the grassland measured | Garske | |
| par.wrongLaiCalculationEnabled | int | switches for activating old LAI calculation | Argentina | |
| par.distributedTraits | array | Desciption of which traits are distributed | Species | |
| par.leafLifeSpans | array | days | leaf life span (group-specific) | SpeciesMono |
| par.lengthOfReferenceVegetationPeriod | array | Fraction of the total year (365 days) which have been considered as the active vegetation period in the reference year(s) | Agostinho | |
| par.maintenanceRespirationPerBiomassFunction | int | Function of maintenance respiration calculation | Agostinho | |
| par.maintenanceRespirationPerBiomassParams | array | Maintainance losses (maintainance respiration & organ renewal & root growth) for different grp | Agostinho | |
| par.maintenanceRespirationRate | float | per | Maintenance respiration rate | SpeciesMono |
| par.maturityAges | array | years | Minimum age of mother plants for producing seeds (group-specific) | SpeciesMono |
| par.negativeGrowthEnabled | int | Whether trees shall shrink if the NPP is negative | HohesHolz_10Species | |
| par.negativeNppBufferEnabled | int | Flag for activating a limitation factor of gross primary productivity as used in older Formind versions | Agostinho | |
| par.nppAllocationsToPlantExudation | array | NPP allocation of a single plant to exudation (group-specific) | GCEF_EM_amb_plotmean | |
| par.nppAllocationsToPlantGrowth | array | NPP allocation of a single plant to shoot (group-specific) | SpeciesMono | |
| par.plantCohortsEnabled | int | switches for activating the cohort approach (default is 1 true, 0 means every cohort is one single plant) | paracouForest_controlPlots_9pft | |
| par.treeRootBiomassFromStemBiomassFactor | float | Linear relationship of root biomass to stem biomass | Core_8pft | |
| Mortality | ||||
| par.sizeDependentMortalityEnabled | int | Flag for activating background mortality | Argentina | |
| par.lifespan | array | years | plant life span (group-specific) | SpeciesMono |
| par.treeFallEnabled | int | Flag for deactivating falling of dying trees | Argentina | |
| Seeds, Reproduction | ||||
| par.seedDispersalKernelLocationParams | array | m | Mean distance of mother trees for dispersing seeds (group-specific) | Core_6pft_seedtree_multiple |
| par.seedDispersalKernelShapeParams | array | m | Maximum distance of mother trees for dispersing seeds (group-specific) | Agostinho |
| par.seedGerminationRates | array | per | Germination rate of seeds (group-specific) | SpeciesMono |
| par.seedGerminationTimes | array | days | Time to emergence of seeds since sowing (group-specific) | SpeciesMono |
| par.seedInflowPredationEnabled | int | switches for density-dependent seed mortality | Agostinho | |
| par.seedMasses | array | t | Biomass of seed (group-specific) | SpeciesMono |
| par.seedPoolPredationEnabled | int | switches for activating the mother plant and seed density dependent seed predation mortality | Agostinho | |
| par.seedPredationEnabled | int | switches for activating the mother plant and seed density dependent seed predation mortality | Agostinho | |
| par.seedPredatorEfficiency | array | m | Seed predator attack efficiency | Agostinho |
| par.seedPredatorHandlingTime | array | m | Seed predator handling time | Agostinho |
| par.seedPredatorNumber | array | m | Total seed predator number in the vicinity of each plant | Agostinho |
| par.seedPulseEnabled | int | Flag for activating pulsed ingrowth of accumulated seeds | Argentina | |
| par.seedSurvivalProbabilities | array | per | Survival rate of seeds (group-specific) | Agostinho |
| par.seedlingHeight | float | m | Height of established seedlings | SpeciesMono |
| par.seedlingIngrowthLimitEnabled | int | Flag for activating the density regulation of establishing seedlings | Argentina | |
| par.seedlingMortalityDensityDependenceEnabled | int | switches for activating density-dependent seedling mortality | Core_6pft_seedtree_multiple | |
| par.seedsPerMotherTree | array | Number of seeds which a mother plant is able to produce per time step (group-specific) | Agostinho | |
| par.shootRootRatio | array | Parameters of shoot-root relationship (group-specific) | SpeciesMono | |
| par.dayOfSeedInfluxStart | float | Starting time of ingrowth of global seeds from outside | SpeciesMono | |
| par.dispersalByAnimalIndicators | array | PFTs which have animal dispersed seeds. These do not throw seeds at the matrix (non forest area). | Agostinho | |
| par.individualSeedProductionEnabled | int | Flag for activating seed ingrowth by simulated mother trees | Argentina | |
| Light | ||||
| par.Light_Comp_Factor | float | Light competition factor for grassmindEnabled, reduces LAI over the plant | Species | |
| par.lightLimitationEnabled | int | Flag for activating light competition | GCEFext | |
| par.radiativeTransferModelEnabled | int | Switch for Radiative transfer Model | HohesHolz_10Species | |
| Soil and Water Processes | ||||
| par.Soil_File | array | Name of soil file(s) of all patches | SpeciesMono | |
| par.Water_KL | float | mm | Interception constant | Agostinho |
| par.Water_L | float | Pore size distribution index | Agostinho | |
| par.Water_LayerDepth | float | m | Constant width of soil layers | Agostinho |
| par.Water_MSW | array | g | Minimum soil water content for maximum uptake, relative to range between PWP and FC (group-specific) | GCEFext |
| par.Water_RainfallDuration | float | hours | Hours of rainfall per day | Agostinho |
| par.Water_SD | float | m | Soil depth | Agostinho |
| par.Water_SoilLayer | int | Number of different soil layers | Agostinho | |
| par.Water_WUE | array | g | Water-use-efficiency-coefficient (group-specific) | Agostinho |
| Climate and Environmental Factors | ||||
| par.CO2_dependency_function_simple | array | polynom(a + bx + cx2 + dx3) for co2 dependency of the photosynthesis | Core_8pft | |
| par.CO2_reference_temperature | float | reference temperature | Core_8pft | |
| par.Temperature_Q10 | float | temperature | Base of the temperature effect (Q10-function) affecting the maintenance respiration of a plant | Agostinho |
| par.Temperature_min | float | temperature | Minimum temperature for calculating the length of the vegetation period of a plant | Agostinho |
| par.Temperature_month_cold | array | temperature | Mean temperature of the coldest month the numSpecies group is able to occur (group-specific) | Agostinho |
| par.Temperature_month_hot | array | temperature | Mean temperature of the warmest month the numSpecies group is able to occur (group-specific) | Agostinho |
| par.Temperature_opt | float | temperature | Optimal temperature for maximum gross photosynthesis of a plant (i.e. mean of the normal distribution) | Agostinho |
| par.Temperature_sig | float | temperature | Standard deviation of the normal distribution affecting maximum gross photosynthesis of a plant when temperature deviates from its optimum | Agostinho |
| par.climateFilePath | string | File name and relative path (to the *.exe) of daily climate data for radiance, air temperature, day-length and potential evapotranspiration | Agostinho | |
| par.climateModulesEnabled | array | Flag for activating the advanced climate (Soil water module; Temperature effects; daily changing radiance; daily changing day-length; vegetation period) | Agostinho | |
| par.climateRandomizationEnabled | int | generalAmazonianForest_3pft | ||
| par.wetSeasonLength | int | day | absolute length of wet season | Argentina |
| par.referenceCo2Concentration | float | reference CO2 concentration | Core_8pft | |
| par.referenceEnvironmentalGppReduction | array | Tree gross photosynthesis reduction due to temperature effects and soil water deficit effect of the reference year(s) | Agostinho | |
| par.referenceStomataCo2Concentration | float | stomata CO2 concentration | Core_8pft | |
| Reproduction and Dispersal | ||||
| par.externalSeedInfluxEnabled | int | Flag for using global seed ingrowth from outside a hectare | Argentina | |
| par.invasionEnabled | array | 0 | Please indicate which numSpecies group is the invasive bamboo numSpecies (set to 1) | Argentina_Bamboo |
| par.invasionTime | int | yrs | Please set the point in time for invasion | Argentina_Bamboo |
| par.randomGeneratorSeedDisabled | int | Flag for activating stochasticity (0: reproducible / 1: NOT reproducible) | Argentina | |
| par.reducedSeedProductionAtEdgeEnabled | int | Flag for activating reduced seed ingrowth by simulated mother trees | Argentina | |
| Modules | ||||
| par.viewZenithAngle | array | grad | angle of the place of the observer in zenith direction | HohesHolz_10Species |
| par.LargeFootprintDiameter | float | meters | Diameter (m) of large lidar footprints | generalAmazonianForest_3pft |
| par.LargeFootprintEnergySD | float | meters | Standard deviation (m) of gaussian horizontal energy distribution within large lidar footprints (recommendation 0.5 times radius) | generalAmazonianForest_3pft |
| par.fireFrequency | float | year | Mean time between two occurring fire events | Core_8pft |
| par.fireMode | int | Choose from different modes in which the fire module runs | virtualAmazon_3pft | |
| par.fireModuleEnabled | int | Flag for activating the fire submodule | Argentina | |
| par.fireSeverity | float | Severity of a fire event (0.1 = low; 1.0 = strong) | Core_8pft | |
| par.fireStartYear | float | year | Year for first potential fire event | virtualAmazon_3pft |
| par.fireToleranceClass | array | fireModuleEnabled tolerance = probability for death (1: no tolerance ... 4: tolerant against fire) (group-specific) | Core_8pft | |
| par.relativeFireSize | float | percent | Mean fire size (as relative area of total simulation area) | Core_8pft |
| par.lianaIndicators | array | lianaModuleEnabled (group-specific) (0: is plant; 1: is liana) | paracouForest_controlPlots_9pft | |
| par.lianaModuleEnabled | int | switches for activating the liana submodule | paracouForest_controlPlots_9pft | |
| Misc | ||||
| par.preInitializationEnabled | int | Flag for activating pre-initialization of light climate and space conditions | Argentina | |
| par.individualSpeciesIdEnabled | int | Flag for activating numSpecies number for each plant | Core_8pft | |
| par.treeListOutputStartTime | float | years | Time for first generation of plant list output (res-file containing each plant with position and cohort-file containing each cohort) | fertile_soil_8pft |
| par.treeListOutputTimeStep | float | years | Time interval between generation of plant list outputs (res-file containing each plant with position and cohort-file containing each cohort) | fertile_soil_8pft |
| par.regenerationOnlyInForestEnabled | int | Switch to allow regeneration only inside the forest when starting with inv file. | HohesHolz_10Species | |
| par.relAzimuthAngle | array | grad | the absolute difference between the azimuth angles of the observer and the sun: abs(SunAzimuth-SensorAzimuth-180) | HohesHolz_10Species |
| par.rhizobiaExchangeRateCToN | float | exchange rate of C amounts to rhizobia to get N amounts | GCEF_EM_amb_plotmean | |
| par.rootDepthParams | array | Parameters of shoot biomass - rooting depth relationship (group-specific) | SpeciesMono | |
| par.rootLifeSpans | array | days | root life span (group-specific) | SpeciesMono |
| par.rtmLeafParameters | array | 1 | Leaf parameters of the radiative transfer model group-specific 1: Cab Chlorophyll a+b content, | HohesHolz_10Species |
| par.rtmSoilWetness | float | degree | Use reflection Profile for: 0 drySoil - 1 wetSoil | HohesHolz_10Species |
| par.smallTreeDbhIncrementAsFractionOfMax | array | Realized increment of stem diameter for smallest plant relative to the maximum increment (group-specific) | Core_8pft | |
| par.smallTreeDbhThresholdForDbhIncrement | array | m | Stem diameter at which yearly increment of stem diameter (group-specific) is calculated by defined function (Growth_Function_Switch) | paracouForest_controlPlots_9pft_DBH1cm |
| par.smallTreeSpaceUsageCapacity | float | Reduces stem number when plant crown area > SpaceLimitation_Factor (Standard: 1 = 100%) for all trees with DBH <= alteredSpaceLimitationDbhThreshold | paracouForest_controlPlots_9pft_DBH1cm | |
| par.specificRootLength | array | Specific root length (group-specific) | SpeciesMono | |
| par.splineApproximationStep | float | m | Minimal possible diameter increment step of trees (only required for lookup approach for asymptotic diameter-height curve) | gifu |
| par.sunZenithAngle | array | grad | angle of the place of the sun in zenith direction | HohesHolz_10Species |
| par.symbioticNitrogenFixationFraction | array | fraction of symbiotic nitrogen fixation (group-specific) | GCEF_EM_amb_plotmean | |
| par.temperatureReductionFunction | string | Type of temperature effect used for reducing gross photosynthesis of a plant | Agostinho | |
| par.traitDistributionEnabled | int | Flag for activating trait distributions | Species | |
| par.traitDistributionPars | array | Mean [0] and sd [1] min [2] and max [3]of the traits adressed in distributedTraits | Species |
State variables
Table 16: Geometrical state variables.
| Symbol | Description | Unit |
|---|---|---|
| $D$ | Stem diameter at breast height | $\text{m}$ |
| $H$ | Height | $\text{m}$ |
| $C_{D}$ | Crown diameter | $\text{m}$ |
| $C_{L}$ | Crown length | $\text{m}$ |
| $C_{A}$ | Crown projection area | $\text{m}^2$ |
| $B$ | Aboveground biomass | $t_{\text{ODM}}$ |
| $LAI$ | Leaf area index | - |
| $\Delta B$ | Biomass increment per time step | $t_{\text{ODM}}$ |
| $\Delta D$ | Diameter increment per time step | $\text{m}$ |
Table 17: Recruitment and establishment state variables.
| Symbol | Description | Unit |
|---|---|---|
| $N_{\text{pool}}$ | Seed pool (i.e number of seeds) | $\tfrac{1}{\text{patch}}$ |
| $N_{\text{germ}}$ | Number of successfully germinated seeds | $\tfrac{1}{\text{patch}}$ |
| $N_{\text{est}}$ | Number of successfully established seedlings | $\tfrac{1}{\text{patch}}$ |
| $x_{\text{ind}}$, $y_{\text{ind}}$ | Random position of a mother tree on a patch | - |
| $x_{\text{seed}}$, $y_{\text{seed}}$ | Position of a dispersed seed | - |
| $I_{\text{floor}}$ | Percentage of incoming irradiance at floor | $\%$ |
Table 18: Mortality state variables.
| Symbol | Description | Unit |
|---|---|---|
| $M_{D}$ | Mortality rate dependent on stem diameter | $\tfrac{1}{\text{yr}}$ |
| $M_{I}$ | Mortality rate dependent on stem diameter increment | $\tfrac{1}{\text{yr}}$ |
| $M$ | Mortality rate affecting individuals each time step | $\tfrac{1}{\text{yr}}$ |
| $m_{\text{frag}}$ | Factor changing the mortality rate $M$ due to fragmentation | - |
| $CCA_{i}$, $i = 1$, $...$, $\#_{\text{layer}}$ | Cumulative crown area per height layer | - |
| $l_{\text{min}}$, $l_{\text{max}}$ | Lower and upper height layer covered by the crown of a single individual | - |
| $R_{c}$ | Individual crowding reduction factor | - |
| $N_{C}$ | Number of individuals dying due to crowding | $\tfrac{1}{\text{cohort}}$ |
| $N_{Y}$ | Number of individuals dying due to mortality per time step | $\tfrac{1}{\text{cohort}}$ |
| $N$ | Number of alive individuals | $\tfrac{1}{\text{cohort}}$ |
| $\Delta _{rM}$ | Auxillary variable | - |
| $N_{F}$ | Number of individuals affected by a falling tree | - |
Table 19: Light climate and growth state variables.
| Symbol | Description | Unit |
|---|---|---|
| $\overline{L_i}$ | Individual leaf area contribution to height layer $i$ | $\text{m}^2$ |
| $\widehat{L_i}$ | Patch-based leaf area index | - |
| $I_{\text{ind}}$ | Incoming irradiance on top of an individual | $\tfrac{\mu\text{mol}_{\text{photon}}}{{\text{m}^2}\text{s}}$ |
| $I_{\text{leaf}}$ | Incoming irradiance on top of the leaf surface (absorbable radiation) | $\tfrac{\mu\text{mol}_{\text{photon}}}{{\text{m}^2}\text{s}}$ |
| $P_{\text{ind}}$ | Gross photosynthetic rate of an individual | $\tfrac{\mu\text{mol}_{\text{CO}_2}}{\text{yr}}$ |
| $P_{\text{leaf}}$ | Gross photosynthetic rate of a single leaf | $\tfrac{\mu\text{mol}_{\text{CO}_2}}{\text{m}^2\text{s}}$ |
| $GPP$ | Gross productivity of an individual (possibly reduced) | $\tfrac{t_{\text{ODM}}}{\text{yr}}$ |
| $R_{m}$ | Maintenance respiration | $\tfrac{t_{\text{ODM}}}{\text{yr}}$ |
| $r_{m}$ | Maintenance respiration rate | $\tfrac{1}{\text{yr}}$ |
Table 20: Water module state variables.
| Symbol | Description | Unit |
|---|---|---|
| $\Theta_{\text{soil}}$ | Soil water content | $\tfrac{\text{mm}}{\text{h}}$ |
| $IN$ | Interception | $\tfrac{\text{mm}}{\text{h}}$ |
| $RO$ | Run-off | $\tfrac{\text{mm}}{\text{h}}$ |
| $RO_{\rightarrow}$ | Surface run-off | $\tfrac{\text{mm}}{\text{h}}$ |
| $RO_{\downarrow}$ | Sub-surface run-off | $\tfrac{\text{mm}}{\text{h}}$ |
| $TR$ | Transpiration | $\tfrac{\text{mm}}{\text{h}}$ |
| $\phi_{W}$ | Reduction factor of $GPP$ due to limited soil water | - |
Table 21: Temperature state variables.
| Symbol | Description | Unit |
|---|---|---|
| $\phi_{\text{act}}$ | Length of vegetation period | $\text{d}$ |
| $\phi_{T}$ | Limitation factor of $GPP$ by temperature | - |
| $\phi_{T,l}, \phi_{T,h}$ | Inhibition factors for low and high temperatures | - |
| $\kappa_{T}$ | Factor affecting maintenance respiration rate $r_{M}$ by temperature | - |
Table 22: Carbon cycle state variables.
| Symbol | Description | Unit |
|---|---|---|
| $S_{\text{dead}}$ | Carbon stock of deadwood | $\tfrac{t_C}{\text{patch}}$ |
| $S_{\text{slow}}$ | Carbon amount of slow decomposing soil stock | $\tfrac{t_C}{\text{patch}}$ |
| $S_{\text{fast}}$ | Carbon amount of fast decomposing soil stock | $\tfrac{t_C}{\text{patch}}$ |
| $S_{\text{mort}}$ | Carbon amount of individuals dying within the current time step | $\tfrac{t_C}{\text{patch}}$ |
| $t_{S_{\text{dead}}\rightarrow A}$ | Transition rate of carbon from deadwood stock $S_{\text{dead}}$ to atmosphere $A$ | $\tfrac{t_C}{\text{patch}}$ |
| $t_{S_{\text{slow}}\rightarrow A}$ | Transition rate of carbon from slow decomposing soil stock $S_{\text{dead}}$ to atmosphere $A$ | $\tfrac{t_C}{\text{patch}}$ |
| $t_{S_{\text{fast}}\rightarrow A}$ | Transition rate of carbon from fast decomposing soil stock $S_{\text{dead}}$ to atmosphere $A$ | $\tfrac{t_C}{\text{patch}}$ |
| $t_{S_{\text{dead}}\rightarrow}$ | Transition rate of carbon from deadwood stock $S_{\text{dead}}$ to soil | $\tfrac{t_C}{\text{patch}}$ |
| $t_{S_{\text{dead}}}\rightarrow S_{\text{slow}}$ | Transition rate of carbon from deadwood stock $S_{\text{dead}}$ to slow decomposing soil stock $S_{\text{slow}}$ | $\tfrac{t_C}{\text{patch}}$ |
| $t_{S_{\text{dead}}}\rightarrow S_{\text{fast}}$ | Transition rate of carbon from deadwood stock $S_{\text{dead}}$ to fast decomposing soil stock $S_{\text{fast}}$ | $\tfrac{t_C}{\text{patch}}$ |
| $NEE$ | Net ecosystem exchange | $\tfrac{t_C}{\text{patch}}$ |
| $C_{GPP}$ | Carbon amount of gross productivity per patch | $\tfrac{t_C}{\text{patch}}$ |
| $C_{R}$ | Carbon amount released by total respiration per patch | $\tfrac{t_C}{\text{patch}}$ |
Table 23: Disturbances (fire, landslide) state variables.
| Symbol | Description | Unit |
|---|---|---|
| $N_{D}$ | Number of individuals dying due to disturbances | $\tfrac{1}{\text{cohort}}$ |
| $P_{F_1}, P_{F_2}, P_{F_3}, P_{F_4}$ | Burning probabilities for the 4 fire tolerance levels | - |
Table 24: Lidar state variables.
| Symbol | Description | Unit |
|---|---|---|
| $d_{\text{Lid}}$ | Number of vegetation voxels above a focal voxel, corresponds to distance that the laser beam traveled within tree canopy space | $\text{m}$ |
| $P_{\text{Lid}}$ | Probability of a voxel to contain a Lidar return | - |
Process order
This file has a copy in the formind/doc/ such that an outdated handbook can be updated easier.
The ordering in the Step() function in the <for_formind.cpp>:
runInitialProcesses()runIntermediateProcesses()(if (!par.preInitializationEnabled))runFinalProcesses()
The code is provided and the concepts of the main functionality.
InitialProcesses
1. resetOutputForTimeStep()
Puts some output variables to zero. (e.g. output.DEATH)
2. initEnvironmentForTimestep()
Checks activated modules and prepares the required structure of the variables environemnt (e.g. sets the required patch.lengthOfVegetationPeriod for environment.isAdvancedClimateActivated())
3. forSeed.doEstablishment()
Does the seeds.
Runs using DeterminePulsedEstablishment() and DetermineGlobalSeedNumber(hec).
4. forDeath.doMortality()
Subroutine for Mortality. All mortality processes over all hectars and plots.
5. doLightCompetition()
Subroutine for all light competition processes.
Using calcLai, calcLightAttenuation and calcSpaceConditions.
6. growth.calcDailyGpp()
Calculates the unreduced GPP on each day in a a year for each plant.
Code
if (timer.isBeginOfYear() || par.grassmindEnabled) resetOutputForTimestep();
initEnvironmentForTimestep();
forSeed.doEstablishment();
if (par.traitDistributionEnabled) traitModule.disperseTraits();
if (par.lianaModuleEnabled) doLiana(patchGrid, switches.layerThickness, forDeath);
forDeath.doMortality();
doLightCompetition();
growth.calcDailyGpp();
IntermediateProcesses
Whatever the time increment is, the water logic is run on a daily basis.
The runIntermediateProcesses() function is overloaded:
In the Step() it is called without argument which means it is looped over every single day with the argument dayIndex which just calls growth.calcDailyWaterForAllPatches(dayIndex).
This does the water availability calculation everywhere.
FinalProcesses
1. growth.doGrowth()
Temperature, water availability etc. reduces GPP, then growth is performed. Loop over all patches and trees which grows each tree according to the calculated GPP.
2. growth.doGrowthProcessesAccounting()
Loop over all patches and trees which keeps track of different characteristic values (e.g., GPP, biomass, biomass lost due to stress) on a patch level.
3. calcAndWriteOutput(0)
Writes outputs.
4. timer.next()
Sets the clock by a timestep.
Code
if (environment.isAdvancedClimateActivated()) {
reduceDailyGpp();
}
if (par.spatiallyExplicitZoneOfInfluenceEnabled) {
calculateCellVector();
}
growth.doGrowth();
growth.doGrowthProcessesAccounting();
if (par.fireModuleEnabled) {
if (timer.isCurrentTimeEqual(par.fireStartYear)) doFire();
if (timer.isCurrentTimeBiggerThan(par.fireStartYear)) {
if (par.fireMode == 0 || par.fireMode == 1) doFire();
}
}
if (par.radiativeTransferModelEnabled) { // timer->getTime()==timer->End
runRtm();
calcRtmOutput();
}
if (par.variableIrradianceEnabled || par.temperatureEffectEnabled || par.vegetationPeriodEnabled ||
par.variableDayLengthEnabled || (par.co2EffectEnabled > 0)) {
if (resultFileSwitch.env) resultWriter.WriteEnvironmentOutput();
}
if (par.soilWaterLimitationEnabled) {
resultWriter.WriteWaterOutput();
if (timer.getStepSize() == 1.0 && resultFileSwitch.water_daily) {
resultWriter.WriteWaterDailyOutput();
}
}
if (par.landslideModuleEnabled) {
doSingleGlobalLandslide(50);
}
if (logging.DoIt) logging.doLogging();
if (logging.Thinning) doThinning();
if constexpr (isGrass<PlantWithTraitsType>) {
logging.isMowedrightnow = false;
logging.mowHeight = 100;
applyMowingRegime(this);
if (par.centuryGrassSoilModelEnabled || par.daycentGrassSoilModelEnabled) {
if (par.externalLandtransSoilModel == 1) {
calculateLitterInputForBodium();
} else if (!par.externalLandtransSoilModel || par.externalLandtransSoilModel == 3) {
calculateCarbonFluxCentury();
}
}
} else {
calcCarbonFlux();
}
calcAndWriteOutput(0);
timer.next();
if (!par.preInitializationEnabled) {
if (logging.Done > 0.0) logging.Done += timer.getStepSize();
}
par.preInitializationEnabled = false;
Abbreviations
| Symbol | Description |
| ODM | Organic dry matter |
| CO2 | Carbon dioxide |
| C | Carbon |
| H2O | Water |
| sin | Sinus function |
| cos | Cosinus function |
| ⌊⌋ | Round down |
| e | Exponential function |
| ln | Logarithm function |
| cf. | see |
| e.g. | exempli gratia (for example) |
| i.e. | id est (that is) |
| Fig. | Figure |
| Tab. | Table |
Bibliography
[botta2000] - Botta, A. and Viovy, N. and Ciais, P. and Friedlingstein, P. and Monfray, P. - A global prognostic scheme of leaf onset using satellite data. - 2000. -
Summary/Abstract
[busing2006] - Busing, Richard T and Solomon, Allen M - Modeling the effects of fire frequency and severity on forests in the northwestern United States. - 2006. -
Summary/Abstract
[dislich2009] - Dislich, C. and Günter, S. and Homeier, J. and Schröder, B. and Huth, A. - Simulating forest dynamics of a tropical montane forest in south ecuador. - 2009. -
Summary/Abstract
[dislich2012] - Dislich, Claudia and Huth, Andreas - Modelling the impact of shallow landslides on forest structure in tropical montane forests. - 2012. -
Summary/Abstract
[Fischer2016] - Fischer, Rico and Bohn, Friedrich and de Paula, Mateus Dantas and Dislich, Claudia and Groeneveld, Juergen and Gutierrez, Alvaro G and Kazmierczak, Martin and Knapp, Nikolai and Lehmann, Sebastian and Paulick, Sebastian and others - Lessons learned from applying a forest gap model to understand ecosystem and carbon dynamics of complex tropical forests. - 2016. -
Summary/Abstract
[Fischer2010] - Fischer, Rico - Modellierung des Wachstums von Regenwäldern. Untersuchung der Auswirkungen von Trockenstress und Holznutzung auf den tropischen Regenwald am Beispiel des RNI Betampona (Madagaskar).. - 2010. -
Summary/Abstract
[fischer2021Fire] - Fischer, Rico - The long-term consequences of forest fires on the carbon fluxes of a tropical forest in Africa. - 2021. -
Summary/Abstract
[gardner1999] - Gardner, Robert H and Romme, William H and Turner, Monica G - Predicting forest fire effects at landscape scales. - 1999. -
Summary/Abstract
[granier1999] - Granier, A. and Bréda, N. and Biron, P. and Villette, S. - A lumped water balance model to evaluate duration and intensity of drought constraints in forest stands. - 1999. -
Summary/Abstract
[green1989] - Green, D. G. - Simulated Effects of Fire, Dispersal and Spatial Pattern On Competition Within Forest Mosaics. - 1989. -
Summary/Abstract
patterns associated with f'we, seed dispersal, and the distributions
of plants and resources affect forest
dynamics profoundly. Simulated fires ignited at random locations in
a uniform environment create
non-uniform habitats and lead to patches dominated by different vegetation
types. Short-range seed
dispersal promotes vegetation clumping; fires cause these clumps to
coalesce into vegetation zones
separated by sharp borders, especially across an environmental gradient.
In simulation of competition
within vegetation mosaics, tree populations with a competitive advantage
still require the intervention of
fire to eliminate rivals. Also, the availability of local seed sources
enables established tree populations
to exclude invaders, but fires can trigger sudden changes in the composition
of such systems. In models
of simple succession systems, 'climax' vegetation tends to displace
'pioneer' vegetation, even under harsh
fire regimes.</div>